Tetraedro

Seja ABCD um tetraedro e considere M;N;O; P os pontos médios das arestas AC;AD;BC;BD respectivamente. Mostre que MNOP é um paralelogramo e obtenha as medidas de seus lados em função das medidas das arestas do tetraedro.

o desenho está mal feito e um pouco porco mas estimo que dê para entender

Considere um cubo (cinza), de aresta L, e o tetraedro formado pelas diagonais reversas das suas faces opostas (preto), de aresta a. Os pontos médios dessas diagonais são as intersecções das diagonais das respectivas faces, i.e., o baricentro daquela face.
Os pontos M, N, O e P escolhidos no enunciado ficam todos sobre um mesmo plano (alfa) que faz um corte no cubo pelo ponto médio das arestas L.


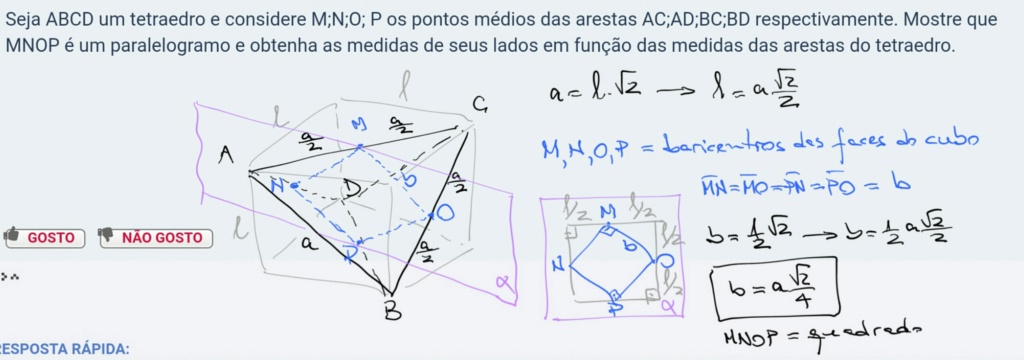
OBS:
consideramos o caso particular de um tetraedro regular (inscrito no cubo) e por isto o paralelogramo MNOP resulta um quadrado. O caso genérico de um tetraedro não regular (que poderia ser inscrito num paralelepípedo) resultaria num paralelogramo. A mecânica é a mesma, basta "alongar" o cubo numa direção ou duas, das três possíveis.

Boa noite Medeiros

MUITO obrigada. Deu p entender sim o desenho

OPS... notei agora: houve ERRO MEU DE CONTA na figura acima. O correto é:

[latex]\\ b = \frac{l}{2}\sqrt{2}\,\,\rightarrow\,\, b = \frac{1}{2}\cdot a\frac{\sqrt{2}}{2}\cdot\sqrt{2}\,\,\rightarrow\,\,\boxed{\,b=\frac{a}{2}\,}[/latex]