angulo de um triangulo isosceles pela lei dos cossenos

Na molécula do metano (CH4), o átomo de carbono central está ligado a átomos de hidrogênio que estão posicionados nos quatro vértices de um tetraedro regular, por isso sua geometria é tetraédrica.

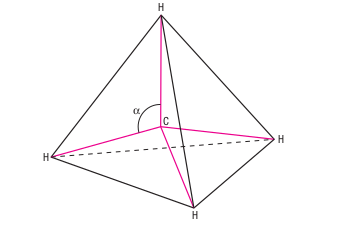
Com base na figura acima, é possível determinar o ângulo (α) entre as ligações covalentes. No entanto, para esse cálculo, seguem algumas informações.
• A distância entre o centro do tetraedro e cada um dos vértices corresponde a [latex]3/4[/latex] da medida de sua altura.
• A medida da altura é igual a [latex]h = \frac{a\sqrt{6}}{3}[/latex] em que a é a medida de cada aresta.

sem gabarito

Olá sbvo76  

Basta aplicar a lei dos cossenos no triângulo vermelho:

[latex]\\a^2=b^2+c^2-2.b.c.\cos\alpha\\\\ \rightarrow\;a^2=2\left ( \frac{3h}{4} \right )^2-2\left ( \frac{3h}{4} \right )^2.\cos\alpha\\\\ \rightarrow\;a^2=2\left ( \frac{3h}{4} \right )^2.(1-\cos\alpha)\\\\ \rightarrow\;\cos\alpha=1-\frac{a^2}{2\left ( \frac{3h}{4} \right )^2}=1-\frac{8}{6}=-\frac{1}{3}\\\\ \rightarrow\;\boxed{\alpha=\arccos(-\frac{1}{3})\cong109,47^o}[/latex]