Quadriláteros
+4
Fibonacci13
rom.vianna@gmail.com
Jose Carlos
wdsx
8 participantes
Página 1 de 1
Quadriláteros
por wdsx Ter 11 Out 2011, 14:04
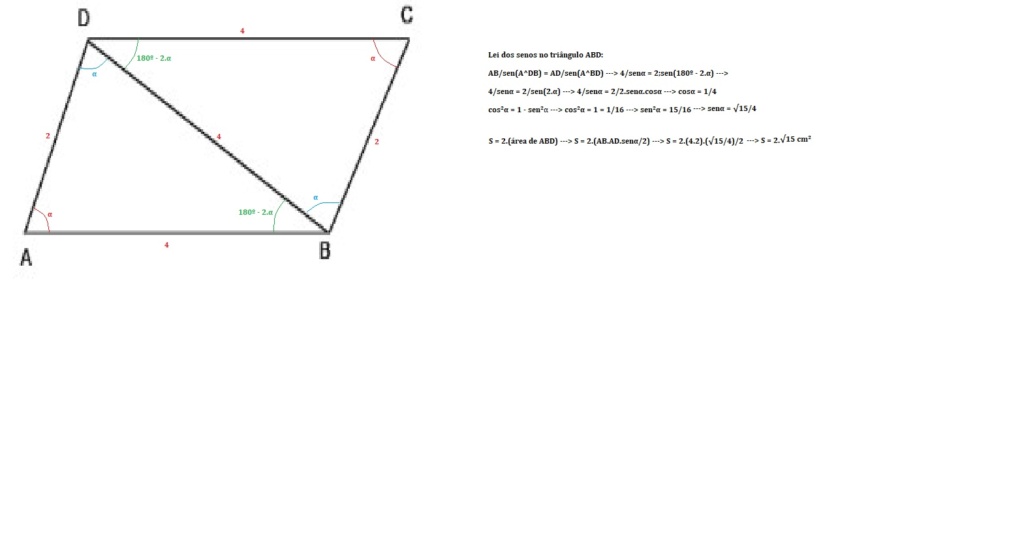
(UFMG) No paralelogramo ABCD, AB=DB=CD, AD=1/2AB. Se AB=4cm, então a área do paralelogramo, em cm^2 é:
https://2img.net/r/ihimg/photo/my-images/706/imagemgkh.jpg/
a) 8
b) 4V2
c) 6V2
d) 6V3
e0 2V15
https://2img.net/r/ihimg/photo/my-images/706/imagemgkh.jpg/
a) 8
b) 4V2
c) 6V2
d) 6V3
e0 2V15
wdsx- Recebeu o sabre de luz
- Mensagens : 174
Data de inscrição : 04/09/2011
Idade : 33
Localização : Belo horizonte, minas gerais , brasil
Re: Quadriláteros
por Jose Carlos Ter 11 Out 2011, 14:23
**Temos:
Triângulo ABD -> altura -> h
h² + 1² = 16 => h² = 15 => h = \/15
S = (2*\/15)/2
S = \/15
Assim a área do paralelogramo será dada por:
S = 2*\/15 cm²
Triângulo ABD -> altura -> h
h² + 1² = 16 => h² = 15 => h = \/15
S = (2*\/15)/2
S = \/15
Assim a área do paralelogramo será dada por:
S = 2*\/15 cm²
Jose Carlos- Grande Mestre
- Mensagens : 5551
Data de inscrição : 08/07/2009
Idade : 74
Localização : Niterói - RJ
Dúvida
por rom.vianna@gmail.com Sex 24 Out 2014, 23:03
Jose Carlos escreveu:**Temos:
Triângulo ABD -> altura -> h
h² + 1² = 16 => h² = 15 => h = \/15
S = (2*\/15)/2
S = \/15
Assim a área do paralelogramo será dada por:
S = 2*\/15 cm²
Olá Carlos,
Ao ler sua resposta fiquei com uma dúvida:
Qual o raciocínio que o levou a colocar o número 1, no Pitágoras?
h² + 1² = 4²
Aproveito para agradecer, desde já, pela atenção.
Muito obrigado.
rom.vianna@gmail.com- Padawan
- Mensagens : 65
Data de inscrição : 26/06/2014
Idade : 35
Localização : belo horizonte -
Re: Quadriláteros
por Fibonacci13 Seg 30 Out 2023, 20:28
Também fiquei com a mesma dúvida.
Figura da questão:
Fibonacci13- Mestre Jedi
- Mensagens : 872
Data de inscrição : 14/09/2019
Idade : 22
Localização : São Paulo
Re: Quadriláteros
por petras Seg 30 Out 2023, 21:01
ELe utilizou duas vezes a área do triangulo ABD cuja altura(h) será a que ele ele calculou.
Como o triângulo é isósceles ele traçou a altura BH e no triÂngulo ABH teríamos base AH = 1, AB = 4 = hipotenusa e a altura o triângulo(HB)
Assim
[latex]2 . S_\triangle ABD = 2.\frac{2.\sqrt15.}{2}=2\sqrt{15}[/latex]
Como o triângulo é isósceles ele traçou a altura BH e no triÂngulo ABH teríamos base AH = 1, AB = 4 = hipotenusa e a altura o triângulo(HB)
Assim
[latex]2 . S_\triangle ABD = 2.\frac{2.\sqrt15.}{2}=2\sqrt{15}[/latex]
Última edição por petras em Seg 30 Out 2023, 22:30, editado 3 vez(es)
____________________________________________
_______________________________
"Ex nihilo nihil fit"
petras- Monitor
- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Giovana Martins e Fibonacci13 gostam desta mensagem
Re: Quadriláteros
por Giovana Martins Seg 30 Out 2023, 21:20
Outro jeito: por Heron.
O semiperímetro do triângulo ABD é dado por:
P = 0,5 x (2 + 4 + 4) = 5 cm
A área do triângulo ABD é dada por:
S² = P x (P - AD) x (P - AB) x (P - BD)
S² = 5 x 3 x 1 x 1 = 15 cm4
S = √15 cm²
A área do paralelogramo é o dobro da área do triângulo ABD, logo, [ABCD] = 2√15 cm².
____________________________________________
Charlotte de Witte - Universal Nation
Giovana Martins- Grande Mestre
- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Fibonacci13 gosta desta mensagem
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Fibonacci13 gosta desta mensagem
Re: Quadriláteros
por Medeiros Ter 31 Out 2023, 02:16
Ainda acho que a melhor resolução é a do colega José Carlos (saudades), contudo segue outro modo bem rasteirinho e sem o brilho das soluções já apresentadas.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Giovana Martins gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
