Geomatria Espacial - Calcular o menor comprimento

Em um terreno plano e horizontal há um mastro vertical e uma linha reta r desenhada no solo e distante alguns metros do mastro.

Pretende-se esticar um cabo de aço ligando o topo do mastro a um ponto dessa linha.

Sem medir os comprimentos, como pode ser determinado o ponto da linha r de forma que o cabo de aço tenha o menor comprimento possível?

Att.

Nilton

trace uma perpendicular à reta r passando pelo pé do mastro. O pé dessa perpendicular é o ponto procurado.

Medeiros, agradeço pela resposta. Mas, ao traçar uma perpendicular à reta R, eu não conseguiria passar pelo pé do mastro... ou eu não entendi a resposta... Consegue demostrar por um desenho? 

Att.

Nilton

Nilton

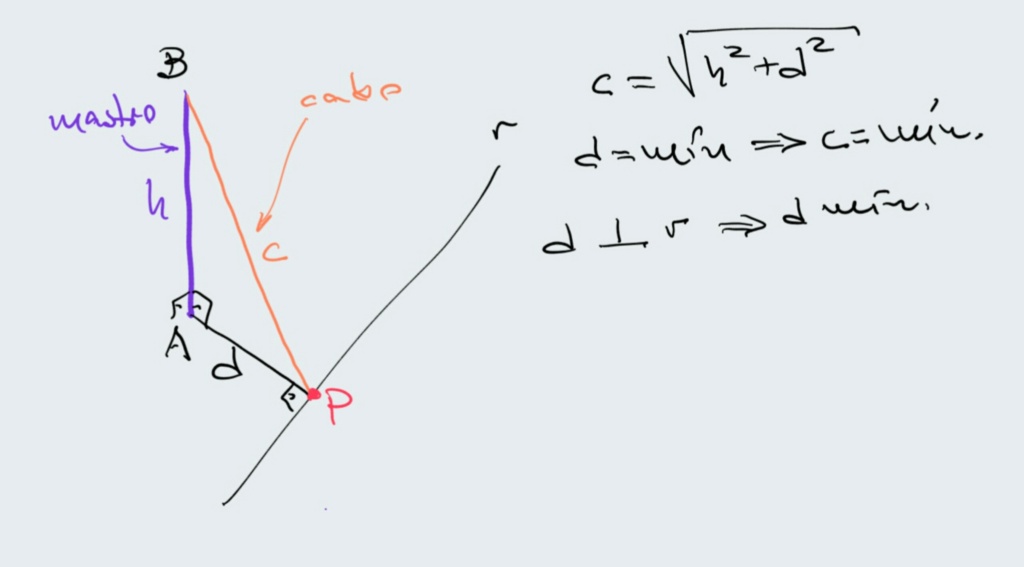
o mastro tem altura fixa e é perpendicular ao solo. Um cabo estendido do alto do mastro até a linha r, em qualquer ponto dela, define um triângulo retângulo onde o cabo é a hipotenusa.

queremos o ponto em r que resulte na menor hipotenusa mas um dos catetos (o mastro) já está definido, então nos sobra somente diminuir o outro cateto o máximo possível -- este é o cateto que fica no chão e vai do pé do mastro até a linha r. Acontece que este cateto será o mais curto quando ele ligar o mastro a r numa linha perpendicular à reta. Onde essa perpendicular chegar em r é o ponto procurado.


Note que a questão pede "sem medir comprimentos, como pode ser determinado o ponto na linha r...". O que eu disse até agora, na mensagem anterior e nesta, foi somente a lógica por trás da solução. Para a resposta ser completa devemos saber traçar, no plano, uma perpendicular a uma reta por um ponto dado. Como isto é muito fácil, assunto do ensino fundamental, eu nada disse; mas se quiser posso mostrar como faz.

Nilton

Você não entendeu foi o enunciado: NÃO foi dito que a reta r passa pelo pé P do mastro

Foi dito que a reta r, no solo, dista alguns metros do pé do mastro (no solo)

Imagine que o pé do mastro fique no meio-fio de um dos passeios de uma rua reta.
E imagine que a reta r é o meio-fio do passeio do outro lado da rua, distante d de P.
O topo do mastro deverá ser ligado num ponto P' da reta r, de modo que PP' = d seja perpendicular a r

Isto significa que a reta r e o mastro (retilíneo) são retas reversas.

situação da questão




problema: pelo ponto A, traçar uma perpendicular a reta r.

A = pé do mastro



Onde falo "compasso", para grandes distâncias vc pode usar uma corda com uma extremidade fixada.

Com uma abertura convenientemente maior do que a distância de A até r coloque a ponta fixa do compasso no ponto A e trace um arco cortando r em dois pontos (X e Y).

Com a ponta seca em X e abertura XY (pode ser abertura maior que a metade da distância XY) trace um arco (ver fig.). Depois com a ponta em Y e igual abertura trace um arco.

O cruzamento destes dois arcos é o ponto Q. O segmento AQ é perpendicular à reta r; marque o ponto P nesse cruzamento.

Medeiros e Elsiochin...

Agradeço imensamente pelas respostas.

Abs.

Nilton