Geometria Plana - Ângulos
Página 1 de 1
Geometria Plana - Ângulos
por bs_estudante Seg 07 Dez 2020, 20:13
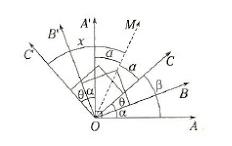
Dados os ângulos consecutivos AOB, BOC e COD, tal que [latex]m\sphericalangle AOC[/latex]<[latex]90^{\circ}[/latex], com centro em O. Gira-se os ângulos a uma medida de [latex]90^{\circ}[/latex], de modo que as novas posições de A, B e C são A', B' e C' e [latex]m\sphericalangle AOC=\beta [/latex]. Se [latex]\overrightarrow{OM}[/latex] é bissetriz do ângulo COA', calcule [latex]m\sphericalangle C'OM[/latex].
a) [latex]45^{\circ} - \frac{\beta }{2}[/latex] b) [latex]30^{\circ} + \frac{\beta }{2}[/latex] c) [latex]45^{\circ} + \frac{\beta }{2}[/latex]
d) [latex]60^{\circ} - \frac{\beta }{2}[/latex]
e) [latex]30^{\circ} - \frac{\beta }{2}[/latex]
Obs.: Não possuo o gabarito
a) [latex]45^{\circ} - \frac{\beta }{2}[/latex] b) [latex]30^{\circ} + \frac{\beta }{2}[/latex] c) [latex]45^{\circ} + \frac{\beta }{2}[/latex]
d) [latex]60^{\circ} - \frac{\beta }{2}[/latex]
e) [latex]30^{\circ} - \frac{\beta }{2}[/latex]
Obs.: Não possuo o gabarito
bs_estudante- Iniciante
- Mensagens : 6
Data de inscrição : 06/02/2020
Tópicos semelhantes» Geometria Plana - Ângulos
» geometria plana-ângulos
» Geometria plana, ângulos
» Geometria plana ( angulos )
» Geometria plana ângulos.
» geometria plana-ângulos
» Geometria plana, ângulos
» Geometria plana ( angulos )
» Geometria plana ângulos.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
