Lei dos cossenos
2 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
 Lei dos cossenos
Lei dos cossenos
(UERJ) A figura 1 representa uma chapa de metal com a forma de um triângulo retângulo isósceles em que AB = BC = CD = 2 m. Dobrando-a nas linhas BE e CE, constrói-se um objeto que tem a forma de uma pirâmide.
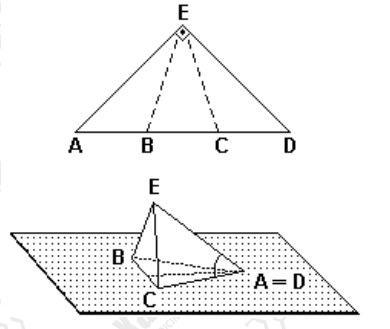
Desprezando a espessura da chapa, calcule o cosseno do ângulo formado pela aresta AE e o plano ABC.

Desprezando a espessura da chapa, calcule o cosseno do ângulo formado pela aresta AE e o plano ABC.
- Resposta:
- Resposta: √6/3 m
Tommy Miller- Iniciante
- Mensagens : 27
Data de inscrição : 03/10/2020

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tommy Miller gosta desta mensagem
 Re: Lei dos cossenos
Re: Lei dos cossenos
Elcioschin escreveu:Uma figura para ajudar:
Elcio, obrigado pela figura. Mas não sei como ela pode me ajudar a encontrar a resposta para o problema. Também não consegui aplicar a lei dos senos na primeira figura, pois não conheço lados nem ângulos suficientes. Até usei lei dos cossenos mas acho que b = √10 m e que a altura do triângulo EBC é 3 m. Poderia me ajudar?
Tommy Miller- Iniciante
- Mensagens : 27
Data de inscrição : 03/10/2020
 Re: Lei dos cossenos
Re: Lei dos cossenos
Pitágoras no triângulo retângulo AED:
AE² + DE² = AD² ---> a² + a² = 6² ---> a² = 18 ---> a = 3.√2 m
Lei dos senos no triângulo AEB:
AE/sen(135º - α) = AB/senα = BE/sen45º --->
a/(sen135º.cosα - cos135º.senα) = 2/senα = b/sen45º
Lei dos senos no triângulo BEC:
BE/sen(α + 45º) = BC/sen(90º - 2.α) ---> b/(senα.cos45º + cosα.cos45º) = 2/2.senα.cosα
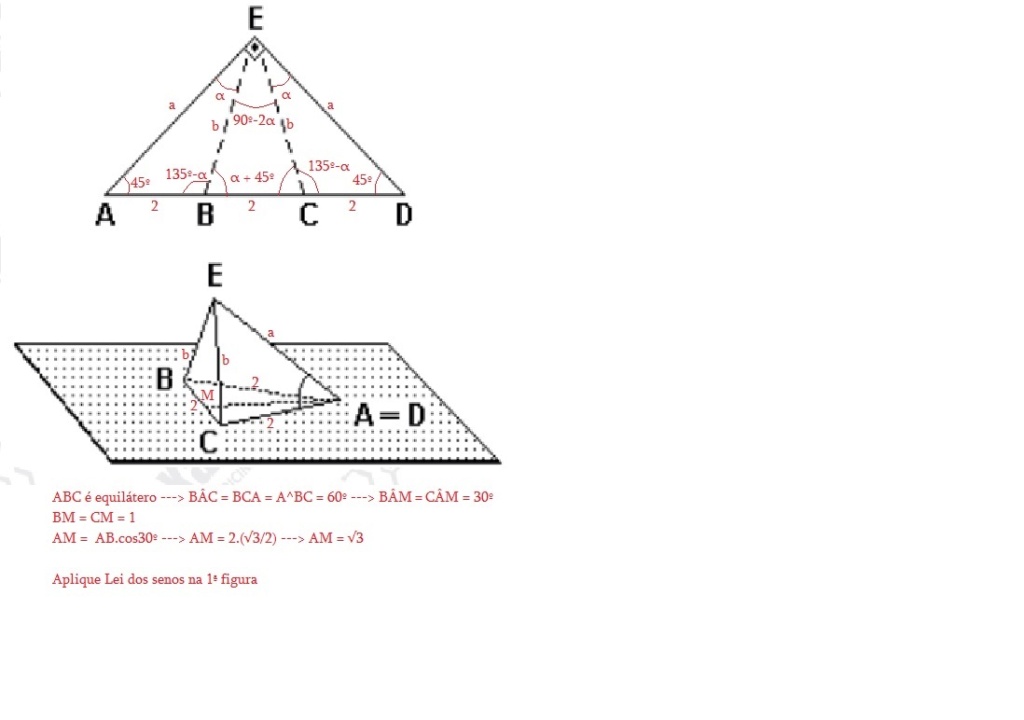
Calculados b, α ---> na 2ª figura calcule EM
No triângulo AEM use lei dos cossenos e calcule cos(EÂM)
As contas são por sua conta.
AE² + DE² = AD² ---> a² + a² = 6² ---> a² = 18 ---> a = 3.√2 m
Lei dos senos no triângulo AEB:
AE/sen(135º - α) = AB/senα = BE/sen45º --->
a/(sen135º.cosα - cos135º.senα) = 2/senα = b/sen45º
Lei dos senos no triângulo BEC:
BE/sen(α + 45º) = BC/sen(90º - 2.α) ---> b/(senα.cos45º + cosα.cos45º) = 2/2.senα.cosα
Calculados b, α ---> na 2ª figura calcule EM
No triângulo AEM use lei dos cossenos e calcule cos(EÂM)
As contas são por sua conta.

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tommy Miller gosta desta mensagem
 Re: Lei dos cossenos
Re: Lei dos cossenos
Elcio, muito obrigado pelo seu desenho e pela sua explicação. infelizmente não consegui chegar no gabarito pela lei dos senos, mas cheguei no gabarito pela lei dos cossenos. Obrigado!
Tommy Miller- Iniciante
- Mensagens : 27
Data de inscrição : 03/10/2020
 Re: Lei dos cossenos
Re: Lei dos cossenos
Então poste o passo-a-passo da sua solução para que outros usuários aprendam contigo!

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tommy Miller gosta desta mensagem
 Re: Lei dos cossenos
Re: Lei dos cossenos
Considerando a sua figura, o triângulo AME é isósceles e tem base 3m e altura 3m, ou seja, o segmento EM tem 3m. O exercício pede o ângulo MÂE do triângulo MAE. Como sabemos seu 3 lados, AM= √3m, ME = 3m e AE = 3√2 , usando a lei dos cossenos descobrimos o cosseno do ângulo pedido.Elcioschin escreveu:Então poste o passo-a-passo da sua solução para que outros usuários aprendam contigo!
Última edição por Tommy Miller em Dom 06 Dez 2020, 18:34, editado 2 vez(es)
Tommy Miller- Iniciante
- Mensagens : 27
Data de inscrição : 03/10/2020
 Re: Lei dos cossenos
Re: Lei dos cossenos
Não entendi
No triângulo AME --->
1) AM = √3
2) AE = a = 3.√2
3) ME é a altura do triângulo isósceles EBC (BE = CE = b)
Para calcular ME você precisa primeiro saber o valor de b
Como você sabe, então, que AME é isósceles?
No triângulo AME --->
1) AM = √3
2) AE = a = 3.√2
3) ME é a altura do triângulo isósceles EBC (BE = CE = b)
Para calcular ME você precisa primeiro saber o valor de b
Como você sabe, então, que AME é isósceles?

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Lei dos cossenos
Re: Lei dos cossenos
Elcioschin escreveu:Não entendi
No triângulo AME --->
1) AM = √3
2) AE = a = 3.√2
3) ME é a altura do triângulo isósceles EBC (BE = CE = b)
Para calcular ME você precisa primeiro saber o valor de b
Como você sabe, então, que AME é isósceles?
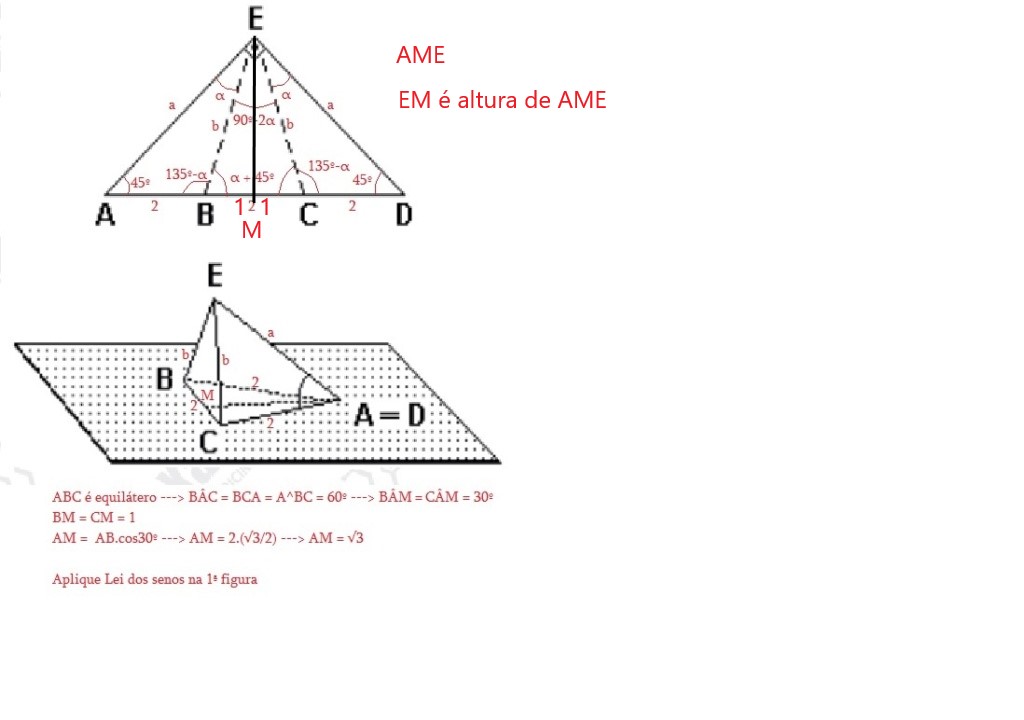
Elcio, tem algo de errado com esse raciocínio? Eu cheguei no gabarito com esse raciocínio. Agradeço pela oportunidade.
Tommy Miller- Iniciante
- Mensagens : 27
Data de inscrição : 03/10/2020
 Re: Lei dos cossenos
Re: Lei dos cossenos
Eu não sei dizer pois vc não mostrou o passo-a-passo dos seus cálculos: só mostrou a que conclusão chegou.

Elcioschin- Grande Mestre

- Mensagens : 73175
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Geometria Plana - Teorema dos Cossenos ou lei dos cossenos
» Lei dos cossenos
» Lei dos cossenos
» Lei dos Cossenos- PT 2
» Lei dos Cossenos
» Lei dos cossenos
» Lei dos cossenos
» Lei dos Cossenos- PT 2
» Lei dos Cossenos
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos