Determinar o maior valor da função

Jeito que eu considero mais fácil por ser mais intuitivo embora a propriedade não seja tão conhecida.

Seja f(x)=325cos(x)+780sin(x)+10, isto é, f(x)=g(x)+10, onde g(x)=325cos(x)+780sin(x). Note que f(x) é tão maior quanto maior for g(x) e tão menor quanto menor for g(x), ou seja, f(x) é variável de acordo com g(x).

Pela Desigualdade de Cauchy-Schwarz:

   [latex]\\\left ( \alpha _1^2+\alpha _2^2+...+\alpha _n^2 \right )\left ( \beta _1^2+\beta _2^2+...+\beta _n^2 \right )\geq \left ( \alpha _1\beta _1+\alpha _2\beta _2+...+\alpha _n\beta _n \right )^2\\\\\mathrm{Para\ o\ nosso\ caso:\ }\left ( \alpha _1^2+\alpha _2^2 \right )\left ( \beta _1^2+\beta _2^2 \right )\geq \left ( \alpha _1\beta _1+\alpha _2\beta _2\right )^2\\\\ \mathrm{Sendo\ }g(x)=325cos(x)+780sin(x):\\\\ \left [ (325)^2+(780)^2 \right ]\left [\underset{1}{ \underbrace{cos^2(x)+sen^2(x)}} \right ]\geq \left [ 325cos(x)+780sin(x) \right ]^2\\\\714025\geq \left [ 325cos(x)+780sin(x) \right ]^2\to |325cos(x)+780sin(x)|\leq 845\\\\\therefore \ -845\leq 325cos(x)+780sin(x)\leq 845\to -845\leq g(x)\leq 845\\\\\therefore g(x)=\pm 845\to\left\{\begin{matrix} f_{min}=-845+10=-835\\ f_{max}=845+10=855 \end{matrix}\right.\ \therefore \ \boxed {f_{max}=855}[/latex]

Truque do triângulo retângulo (solução alternativa).



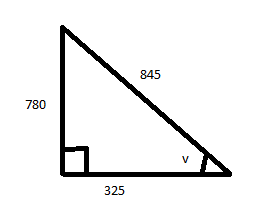
Seja g(x)=780sen(x)+325cos(x).

   [latex]\\\mathrm{Sendo:\ }sen(v)=\frac{780}{845}\ \mathrm{e}\ cos(v)=\frac{325}{845}\\\\g(x)=780sen(x)+325cos(x)\to g(x)=845\left [\frac{780}{845}sen(x)+\frac{325}{845}cos(x) \right ]\\\\g(x)=845[sen(v)sen(x)+cos(v)cos(x)]\to g(x)=845cos(v-x)\\\\\mathrm{Mas:\ }-1\leq cos(v-x)\leq 1\ \therefore \ g(x)=\left\{\begin{matrix} g_{min}=845.(-1)=-845\\ g_{max}=845.1=845 \end{matrix}\right.\\\\f(x)=\left\{\begin{matrix} f_{max},\ \mathrm{se}\ g(x)=g_{max}\\ f_{min},\ \mathrm{se}\ g(x)=g_{min} \end{matrix}\right.\ \therefore \ g(x)=\pm 845\to \left\{\begin{matrix} f_{min}=-845+10=-835\\ \boxed {f_{max}=845+10=855} \end{matrix}\right.\\\\[/latex]

Nota: o truque do triângulo retângulo é muito famoso. Veja maiores explicações aqui: https://pir2.forumeiros.com/t150465-o-truque-do-triangulo-retangulo

Por derivadas sempre fica elegante também .