Período da função

por Cristina Lins Ter 13 Out 2020, 18:38

Qual o período da função h(x) = cos^6 x + sen^6 x?

What do you want to do ?
New mail
Copy

por raibolt Ter 13 Out 2020, 20:45

Existe uma forma de fazer seguindo o princípio fundamental da trigonometria:

sen²(x) + cos²(x) = 1 --- eleva-se os dois lados ao cubo:

$Período da função Gif$ (x) + $Período da função Gif$ (x) + 3. $Período da função Gif$ . sen²(x)+3.cos²(x). $Período da função Gif$ (x) = 1³

$Período da função Gif$ (x) + $Período da função Gif$ (x)+ 3. sen²(x). cos²(x) ]sen²(x)+cos²(x)] = 1 (3sen² . cos² em evidência)

$Período da função Gif$ (x) + $Período da função Gif$ (x)+3. $Período da função Gif$ =1

Conclui-se que:

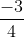$Período da função Gif$ (x) + $Período da função Gif$ (x) = $Período da função Gif$ sen²(2x) +1

Note que o período dessa função encontrada será π/2 já que o valor será 1 quando x= 0 e x = π/2

por pepelinear Ter 13 Out 2020, 22:17

Boa noite colegas! Pensei em outra maneira de fazer; por cálculo, derivando a função dada e igualando-a a zero, para que achemos os máximos e mínimos da função:
h(x) = cos^6 x + sen^6 x
h'(x) = 6.(cos^5 x).( - sen x) + 6.(sen^5 x).(cos x) = 0
Colocando 6.(cos x).(sen x) em evidência:
6.(cos x).(sen x).(sen⁴ x - cos⁴ x) = 0

Assim, os pontos de máximo e mínimo são:
x = π/4.n; com n∈ℤ

Tomando a segunda derivada, para saber quais dos pontos determinados são de máximo ou de mínimo:
h''(x) = 30.(cos⁴ x).(sen² x) - 6.(cos^6 x) + 30.(sen⁴ x).(cos² x) - 6.(sen^6 x).

Testando os pontos x = 0, x = π/4; temos:
h''(0) = 30.0 - 6.(1) + 30.0 - 6.0 = - 6 < 0 → o ponto x = 0 é ponto de máximo da função.
h''(π/4) = 30.(1/4).(1/2) - 6.(1/ Cool

+ 30.(1/4).(1/2) - 6.(1/ Cool

= 6 > 0 → o ponto x = π/4 é ponto de mínimo da função.

Assim, pela análise das derivadas, é perceptível que os pontos x = 0 e x = π/4 são pontos de máximo e mínimo, respectivamente; e, uma vez que a diferença entre eles equivale à metade do período p da função, temos:
1/2.p = π/4 - 0 → p = π/2.
Portanto, o período da função é π/2.

Esta resolução não é de forma alguma mais prática ou vantajosa do que a já apresentada acima; só quis mostrá-la porque me encontro no processo de aprendizagem de análise de funções por derivadas, e achei uma boa oportunidade para testar essas teorias. Caso haja algum equívoco no meu raciocínio, favor apontar.