(FATEC-2010)Trigonómetria
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 (FATEC-2010)Trigonómetria
(FATEC-2010)Trigonómetria
Sejam a e b números reais tais que o sistema, nas incógnitas x e y, 
admite uma única solução. Nessas condições, pode-se afirmar que, sendo k um número inteiro,
a) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]π/2
b) b[latex]\neq [/latex]a+π/2+k[latex]\cdot [/latex]2π/3
c) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]2π/3
d) b[latex]\neq [/latex]a+π/2+k[latex]\cdot [/latex] r
e) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]π

admite uma única solução. Nessas condições, pode-se afirmar que, sendo k um número inteiro,
a) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]π/2
b) b[latex]\neq [/latex]a+π/2+k[latex]\cdot [/latex]2π/3
c) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]2π/3
d) b[latex]\neq [/latex]a+π/2+k[latex]\cdot [/latex] r
e) b[latex]\neq [/latex]a+k[latex]\cdot [/latex]π
- GAB:
- GAB:E
Última edição por AspiraDedeu em Qui 10 Set 2020, 14:46, editado 2 vez(es)

AspiraDedeu- Jedi

- Mensagens : 298
Data de inscrição : 06/07/2020
Idade : 22
Localização : João Pessoa-Paraíba
 Re: (FATEC-2010)Trigonómetria
Re: (FATEC-2010)Trigonómetria
Não sei bem se era esse o caminho e também não tenho o gabarito, mas aqui vai minha tentativa =)
Com o (a) e o (b) fixos acredito que, esse sistema, não sendo impossível, fatalmente, terá apenas uma única solução, logo acredito que tenhamos apenas que mostrar a relação entre a e b que não torne o sistema impossível
Somando as equações temos:
x(cosa + cosb) + y(sena + senb) = constante; usando transformação soma/produto
2x.cos[(a+b)/2].cos[(a-b)/2] + 2y.sen[(a+b)/2].cos[(a-b)/2] = constante
cos[(a-b)/2] {2xcos[(a+b)/2] + 2ysen[(a+b)/2]} = constante
Temos que se cos[(a-b)/2] = 0 o sistema não terá solução
então temos (a-b)/2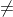 π/2 + k'π
π/2 + k'π
a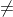 b + π + 2k'π
b + π + 2k'π
a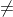 b + kπ
b + kπ
Acho que é isso, ou pelo menos algo parecido.
A minha suposição lá do começo acredito que seja provada por aquela teoria de matrizes de SI SPI e SPD, mas não me lembro bem como fazer ela
Com o (a) e o (b) fixos acredito que, esse sistema, não sendo impossível, fatalmente, terá apenas uma única solução, logo acredito que tenhamos apenas que mostrar a relação entre a e b que não torne o sistema impossível
Somando as equações temos:
x(cosa + cosb) + y(sena + senb) = constante; usando transformação soma/produto
2x.cos[(a+b)/2].cos[(a-b)/2] + 2y.sen[(a+b)/2].cos[(a-b)/2] = constante
cos[(a-b)/2] {2xcos[(a+b)/2] + 2ysen[(a+b)/2]} = constante
Temos que se cos[(a-b)/2] = 0 o sistema não terá solução
então temos (a-b)/2
a
a
Acho que é isso, ou pelo menos algo parecido.
A minha suposição lá do começo acredito que seja provada por aquela teoria de matrizes de SI SPI e SPD, mas não me lembro bem como fazer ela
 Re: (FATEC-2010)Trigonómetria
Re: (FATEC-2010)Trigonómetria
gustavodiniz, desculpa postei tão rapido que nem percebe a falta do gabarito,mas você acertou o gabarito é E

AspiraDedeu- Jedi

- Mensagens : 298
Data de inscrição : 06/07/2020
Idade : 22
Localização : João Pessoa-Paraíba

AspiraDedeu- Jedi

- Mensagens : 298
Data de inscrição : 06/07/2020
Idade : 22
Localização : João Pessoa-Paraíba
 Re: (FATEC-2010)Trigonómetria
Re: (FATEC-2010)Trigonómetria
Então, no [π + 2k'π], por desatenção, achei que dava para conseguir valores impares de pares de π, então chamei de kπ
mas na verdade só se consegue valores impares com essa expressão, o fato de a ter que ser diferente de b + 2k''π vem da parte de sistemas lineares que falei que não lembrava, pesquisei, e para o sistema existir a determinante do sistema tem que ser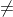 0
0
então temos: cosa.senb - sena.cosb = sen[b-a]
então agora sim, temos a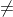 b + 2k''π
b + 2k''π
com: a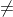 b + 2k''π
b + 2k''π
e a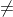 b + π + 2k'π
b + π + 2k'π
temos finalmente: a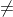 b + kπ
b + kπ
mas na verdade só se consegue valores impares com essa expressão, o fato de a ter que ser diferente de b + 2k''π vem da parte de sistemas lineares que falei que não lembrava, pesquisei, e para o sistema existir a determinante do sistema tem que ser
então temos: cosa.senb - sena.cosb = sen[b-a]
então agora sim, temos a
com: a
e a
temos finalmente: a
 Tópicos semelhantes
Tópicos semelhantes» FATEC - Trigonometria
» Trigonometria FATEC
» Fatec 2009 - trigonometria
» [Resolvido](Fatec) Trigonometria no Paralelogramo
» [Resolvido] TRIGONOMETRIA Parte I: Ajuda para resolver questões de trigonometria
» Trigonometria FATEC
» Fatec 2009 - trigonometria
» [Resolvido](Fatec) Trigonometria no Paralelogramo
» [Resolvido] TRIGONOMETRIA Parte I: Ajuda para resolver questões de trigonometria
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













