Triângulo e Círculo

Boa tarde, senhores!

Preciso de ajuda nessa daqui:

Seja ABC um triângulo tal que os lados AB, BC e AC são respectivamente proporcionais a 6, 3 e 4. Considere o círculo circunscrito ao triângulo, e seja P um ponto do menor arco AC. Se PA=2a, PB=3a, qual o valor de PC?

Gab.: a:

Algumas dicas:

Outra ideia.

Se o triângulo fosse pitagórico, ou seja na relação 3-4-5, o ângulo em C seria reto e AB seria hipotenusa e diâmetro. Como o lado de proporconalidade 6 é maior que 5 então o ângulo em C é obtuso e consequentemente o triângulo está inscrito em menos do que um semicírculo -- conforme o Élcio adequadamente desenhou.

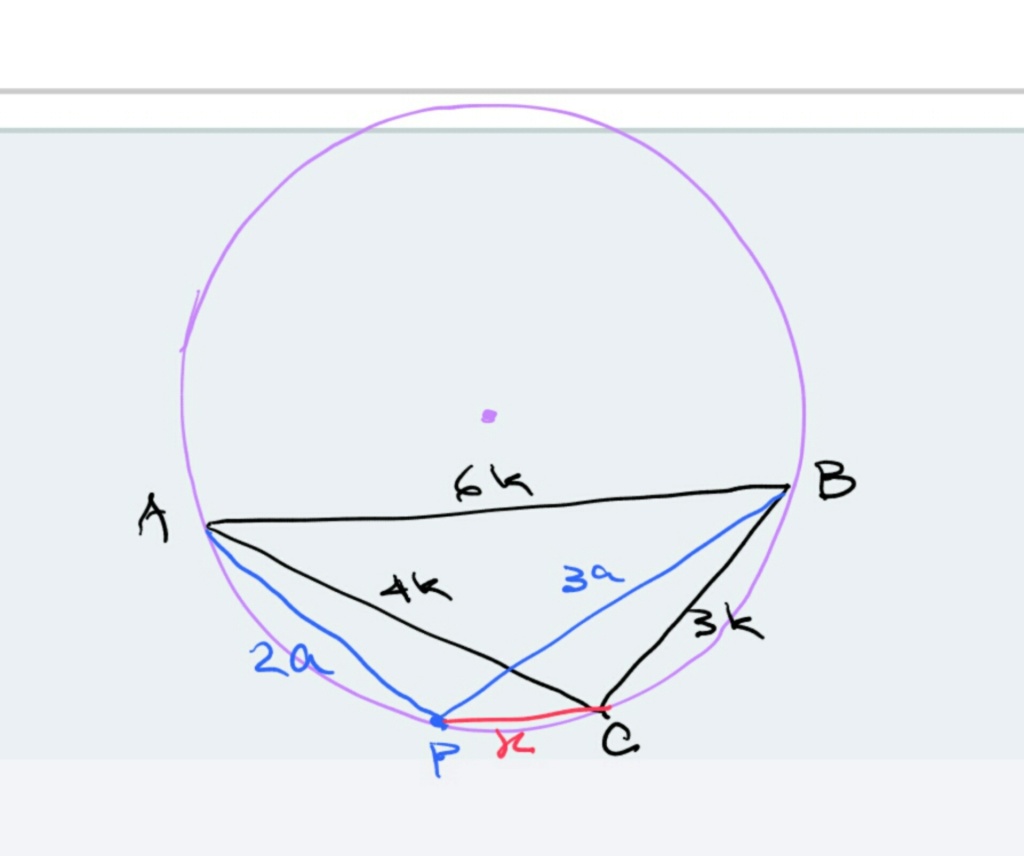
O quadrilátero ABCD está inscrito num círculo, podemos aplicar o
teorema de Ptolomeu: o produto das diagonais é igual a soma do produto dos lados opostos.

AC•PB = AB•PC + AP•BC
4k.3a = 6k.x + 3k.2a
12ka = 6kx + 6ka  ----->  6ka = 6kx  ----->  x = a

_______________________________________________

desejando, podemos obter uma relação entre k e a mediante o teorema de Ptolomeu-Hiparco: a razão entre as diagonais é igual a razão da soma dos produtos dos lados que concorrem com as respectivas diagonais.
\\\frac{4k}{3a} = \frac{6k.2a + 3k.x}{6k.3k + 2a.x}
onde substituindo o já encontrado x=a e fazendo algumas contas devemos chegar em \frac{a}{k} = \frac{4 \sqrt{2}}{\sqrt{37}} ~= 0,93, se não me falha a memória.