Olimpíada Internacional de Matemática (IMO)

São dados um plano \pi , um ponto P pertencente a \pi , e um ponto Q que não pertencente a \pi .Determine todos os pontos R do plano, tais que o quociente 
\frac{(QP+PR)}{QR} seja máximo.

Seja T a projeção ortogonal do ponto Q no plano π. Então, a linha PT é a projeção ortogonal da linha PQ no plano π e, portanto, forma o menor ângulo com a linha PQ entre todas as linhas no ponto P que estão no plano π; portanto,  ∠RPQ  ≥ ∠TPQ , e a igualdade vale se e somente se o ponto R estiver no raio EN (a única exceção é quando  PQ ⊥ π; nesse caso, P = T, então o raio EN é indefinido e a igualdade é válida para todos os pontos R no plano π, pois sempre temos ∠RPQ = ∠TPQ = 90 °).

Em ∠RPQ ≥ ∠TPQ , segue-se que ∠RPQ/2 ≥  ∠TPQ; Além disso, uma vez que os ângulos ∠RPQ e ∠TPQ são <180 °, a metade de seus ângulos ∠RPQ/2  e ∠TPQ/2  são <90 °, de modo que de ∠RPQ/2 ≥ ∠TPQ/2  podemos concluir que sin∠RPQ/2 ≥  sin ∠TPQ /2. A igualdade é válida, como acima, se e somente se o ponto R estiver no raio EN (e, respectivamente, para todos os pontos R no plano π se PQ ⊥ π ).

Por outro lado, obviamente temos cos ( QRP- ∠PQR)/2 ≤ 1 com igualdade se e somente se (∠QRP- ∠ PQR)/2 = 0° , ou seja, se e somente se ∠QRP = ∠PQR,ou seja, se e somente se o triângulo PQR for isósceles com a base QR, ou seja, se e somente se PR = PQ, ou seja, se e somente se o ponto R estiver na esfera com o centro P e o raio PQ.

Agora, aplicando o teorema de Mollweide no triângulo QPR, obtemos
 
                                                                   
                                                           
                                                            

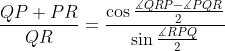
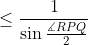
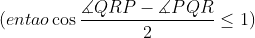
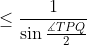
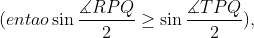
e igualdade se mantém aqui se, e somente se, se houver igualdade nas duas desigualdades sin ∠ RPQ/2 ≥ sin ∠TQP/2 e cos (∠QRP - ∠PQR)/2 ≤ 1 que usamos, ou seja, se e somente se o ponto R estiver tanto no raio EN (essa condição deve ser ignorada se  PQ ⊥ π) quanto na esfera com centro P e raio PQ.

Portanto, o ponto R para o qual a razão (QP + PR)/QR  é máxima é o ponto de interseção do raio EN com a esfera com centro P e raio PQ (ou, respectivamente, pode ser qualquer ponto arbitrário na interseção do plano π com a esfera com centro P e raio PQ se  PQ ⊥ π).