(EN-2007/2008)
3 participantes
Página 1 de 1
 (EN-2007/2008)
(EN-2007/2008)
Considere a função f, de variável real x, definida por f(x)=sen6x+cos6x+m(sen4x+cos4x), onde m∈ℝ é um valor que torna f constante. A equação da circunferência tangente ao eixo y, cujo centro está no ponto de interseção das retas -2mx+2y-5=0 e -x+4y-3=0 é:
A)x2+y2+2x-2y+1=0
B)x2+y2+2x+2y+1=0
C)x2+y2-2x=0
D)x2+y2+2x=0
E)x2+y2-2x-2y+1=0
Desde já, agradeço!
A)x2+y2+2x-2y+1=0
B)x2+y2+2x+2y+1=0
C)x2+y2-2x=0
D)x2+y2+2x=0
E)x2+y2-2x-2y+1=0
Desde já, agradeço!

Eduardo Freitas 3007- Iniciante
- Mensagens : 16
Data de inscrição : 10/12/2015
Idade : 28
Localização : São Pedro da Aldeia RJ Brasil
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
Acho que é assim que se faz.
Se f torna a função constante temos então que a deriavada de f é igual a zero (derivada de uma constante é igual a zero), deriavando f em relação a x vc irá encontrar o valor de m, após isso substitua m no sistema e resolva ele, perceba que se a circunferência é tangente ao eixo y então seu raio é igual a cordenada x do seu centro, dai usa a fórmula ( x - xo) + (y - yo) = r^2, e chegue na resposta.
Se tiver dúvida é só perguntar, estou em aula, então não dá para fazer os cálculos agora hehe.
Se f torna a função constante temos então que a deriavada de f é igual a zero (derivada de uma constante é igual a zero), deriavando f em relação a x vc irá encontrar o valor de m, após isso substitua m no sistema e resolva ele, perceba que se a circunferência é tangente ao eixo y então seu raio é igual a cordenada x do seu centro, dai usa a fórmula ( x - xo) + (y - yo) = r^2, e chegue na resposta.
Se tiver dúvida é só perguntar, estou em aula, então não dá para fazer os cálculos agora hehe.
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
Obrigado pela ajuda, vou tentar, qualquer coisa pergunto novamente
Obrigado pela atenção!
Obrigado pela atenção!

Eduardo Freitas 3007- Iniciante
- Mensagens : 16
Data de inscrição : 10/12/2015
Idade : 28
Localização : São Pedro da Aldeia RJ Brasil
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
Perdão pelo incomodo, eu tentei por calculo e não consegui achar algo exato, com certeza deve ser alguma desatenção minha.
Obrigado pela ajuda!
Obrigado pela ajuda!

Eduardo Freitas 3007- Iniciante
- Mensagens : 16
Data de inscrição : 10/12/2015
Idade : 28
Localização : São Pedro da Aldeia RJ Brasil
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
A derivada de ) , é igual a, e manipulando um pouco:
, é igual a, e manipulando um pouco:
Lembrando que a² - b² = (a - b)(a + b) e que sen²x + cos²x = 1
\\senx.cosx.(6.(sen^4x-cos^4x)+4m.(sen^2x-cos^2x))\\senx.cosx.(6.(sen^2x-cos^2x).(sen^2x+cos^2x)+4m.(sen^2x-cos^2x))\\senx.cosx.(sen^2x-cos^2x).(6+4m))
Como queremos que a derivada seja 0, e queremos descobrir o valor de m, então só nos interessa o caso em que 6 + 4m = 0, ou seja m = -3/2, dessa forma substituindo em -2mx + 2y - 5 = 0, iremos encontrar que 3x + 2y - 5 = 0, junto com o -x + 4y - 3 = 0 iremos encontrar que x = 1 e y = 1.
Sendo a circunferência tangente ao eixo y, temos que seu raio é igual a 1.
Aplicando esses valores na equação da circunferência:
(x - 1)² + (y - 1)² = 1
x² - 2x + 1 + y² - 2y + 1 = 1
x² + y² - 2x - 2y + 1 = 0
Dando como resposta a letra E.
Qualquer dúvida é só perguntar.
Lembrando que a² - b² = (a - b)(a + b) e que sen²x + cos²x = 1
Como queremos que a derivada seja 0, e queremos descobrir o valor de m, então só nos interessa o caso em que 6 + 4m = 0, ou seja m = -3/2, dessa forma substituindo em -2mx + 2y - 5 = 0, iremos encontrar que 3x + 2y - 5 = 0, junto com o -x + 4y - 3 = 0 iremos encontrar que x = 1 e y = 1.
Sendo a circunferência tangente ao eixo y, temos que seu raio é igual a 1.
Aplicando esses valores na equação da circunferência:
(x - 1)² + (y - 1)² = 1
x² - 2x + 1 + y² - 2y + 1 = 1
x² + y² - 2x - 2y + 1 = 0
Dando como resposta a letra E.
Qualquer dúvida é só perguntar.
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
Um outro método sem usar derivadas:
Usando as propriedades de produtos notáveis (a+b)² e (a+b)³ :
(a+b)²:

(a+b)³:

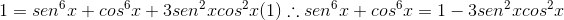
Agora substituindo na função e fazendo as multiplicações temos:
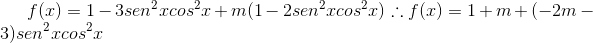
Para que a função independa de x precisamos que -2m-3=0 , para isso temos que m=-3/2
Retas: I) -2(-3/2)x+2y-5=0
3x+2y=5
y=(5-3x)/2
Agora já substuindo y na segunda reta:
II)-x+2(5-3x)-3=0
-x+10-6x=3
-7x=-7
x=1, então y também vale 1
C(1,1), como a questão diz que a circunferência tangencia o eixo y podemos dizer que o raio vale 1 também.
(x-1)²+(y-1)=1²
x²-2x+1+y²-2y+1=1
x²+y²-2x-2y+1=0
Espero ter ajudado!!
Usando as propriedades de produtos notáveis (a+b)² e (a+b)³ :
(a+b)²:

(a+b)³:

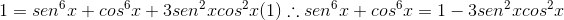
Agora substituindo na função e fazendo as multiplicações temos:
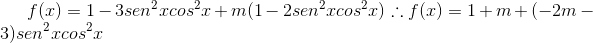
Para que a função independa de x precisamos que -2m-3=0 , para isso temos que m=-3/2
Retas: I) -2(-3/2)x+2y-5=0
3x+2y=5
y=(5-3x)/2
Agora já substuindo y na segunda reta:
II)-x+2(5-3x)-3=0
-x+10-6x=3
-7x=-7
x=1, então y também vale 1
C(1,1), como a questão diz que a circunferência tangencia o eixo y podemos dizer que o raio vale 1 também.
(x-1)²+(y-1)=1²
x²-2x+1+y²-2y+1=1
x²+y²-2x-2y+1=0
Espero ter ajudado!!

RodrigoA.S- Elite Jedi

- Mensagens : 449
Data de inscrição : 12/07/2017
Idade : 25
Localização : Nova Iguaçu
Lucas_DN684 gosta desta mensagem
 Re: (EN-2007/2008)
Re: (EN-2007/2008)
Excelente execução, parabéns e muito obrigado. Tinha conseguido realizar a derivada, porém por alguma desatenção não estava desenvolvendo o produto notável corretamente. Muito obrigado pela paciência, entendi tudo certinho. Abraço.

Eduardo Freitas 3007- Iniciante
- Mensagens : 16
Data de inscrição : 10/12/2015
Idade : 28
Localização : São Pedro da Aldeia RJ Brasil
 Tópicos semelhantes
Tópicos semelhantes» CMR (2007/2008)
» EN 2007/2008 - QUESTÃO 1
» CMS 2007/2008 função
» (IME 2007/2008) Expressão
» Matemática:Trigonometria(Espcex-2007/2008)
» EN 2007/2008 - QUESTÃO 1
» CMS 2007/2008 função
» (IME 2007/2008) Expressão
» Matemática:Trigonometria(Espcex-2007/2008)
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












