Área da região triangular
2 participantes
Página 1 de 1
 Re: Área da região triangular
Re: Área da região triangular
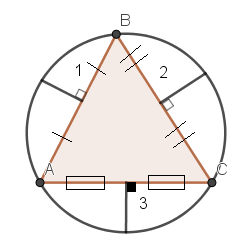
Amigo a figura esta mal elaborada, poderia me explicar se os números (1,2,3) realmente se referem a metade dos respectivos lados ?

LuizLMA- Recebeu o sabre de luz

- Mensagens : 176
Data de inscrição : 24/05/2017
Idade : 25
Localização : Feira de Santana - Ba - Brasil
 Re: Área da região triangular
Re: Área da região triangular
LuizLMA escreveu:Amigo a figura esta mal elaborada, poderia me explicar se os números (1,2,3) realmente se referem a metade dos respectivos lados ?
Sim, caso tenha dificuldade em interpretar a figura apresentada no post... Logo, vc pode visualizar a figura original tbm presente na postagem.
Convidado- Convidado
 Re: Área da região triangular
Re: Área da região triangular
Não foi isto que o colega LuizLMA perguntou.
Ele que saber o que significa 1, 2, 3
São as metades de cada lado do triângulo ou são as distâncias do ponto médio de cada lado até a circunferência?
.
Na minha opinião é a 2ª hipótese: distâncias do ponto médio de cada lado até a circunferência.
Motivo: se um lado do triângulo vale 2, outro 4 e outro 6, esta triângulo é impossível
Note que os prolongamentos dos segmentos 1, 2, 3 se encontram no centro O da circunferência e sejam D, E, F os pontos onde 1, 2, 3 encontram a circunferência
Faça M = ponto médio de AB, N o ponto médio de BC e P ponto médio de AC
OA= OB = OC = OD = OE = OF = R
MD = 1, NE = 2, = PF = 3 --->
OM = OD - MD ---> OM = R - 1
ON = OE - NE ---> ON = R - 2
OP = OF - OF ---> OP = 3 - R
Faça AM = BM = a ---> BN = CN = b, AP = CP = c
Aplique Pitágoras e calcule a, b. c ---> lados do triângulo: 2.a, 2.b, 2.c ---> Calcule área por Herão
Ele que saber o que significa 1, 2, 3
São as metades de cada lado do triângulo ou são as distâncias do ponto médio de cada lado até a circunferência?
.
Na minha opinião é a 2ª hipótese: distâncias do ponto médio de cada lado até a circunferência.
Motivo: se um lado do triângulo vale 2, outro 4 e outro 6, esta triângulo é impossível
Note que os prolongamentos dos segmentos 1, 2, 3 se encontram no centro O da circunferência e sejam D, E, F os pontos onde 1, 2, 3 encontram a circunferência
Faça M = ponto médio de AB, N o ponto médio de BC e P ponto médio de AC
OA= OB = OC = OD = OE = OF = R
MD = 1, NE = 2, = PF = 3 --->
OM = OD - MD ---> OM = R - 1
ON = OE - NE ---> ON = R - 2
OP = OF - OF ---> OP = 3 - R
Faça AM = BM = a ---> BN = CN = b, AP = CP = c
Aplique Pitágoras e calcule a, b. c ---> lados do triângulo: 2.a, 2.b, 2.c ---> Calcule área por Herão

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Área da região triangular
Re: Área da região triangular
Stanford University escreveu:LuizLMA escreveu:Amigo a figura esta mal elaborada, poderia me explicar se os números (1,2,3) realmente se referem a metade dos respectivos lados ?
Sim, caso tenha dificuldade em interpretar a figura apresentada no post... Logo, vc pode visualizar a figura original tbm presente na postagem.
"Não foi isto que o colega LuizLMA perguntou." (Élcio)
Eu disse "sim" para pergunta dele. Além disso, até aconselhei clicar na figura original já que ele não gostou da outra figura. Mas pela sua explanação acima vejo que eu estava equivocado no meu "Sim".
Convidado- Convidado
 Tópicos semelhantes
Tópicos semelhantes» área da região triangular
» Área de região triangular
» Calcular a área da regiao triangular
» Área Triangular
» áre da região triangular
» Área de região triangular
» Calcular a área da regiao triangular
» Área Triangular
» áre da região triangular
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos