Equação Segmentária da Reta
2 participantes
Página 1 de 1
Equação Segmentária da Reta
por Luana Skywalker Sex 01 Dez 2017, 17:14
1-Os pontos A, B, C, D, E e F determinam um hexágono regular ABCDEF de lado 1, tal que o ponto A tem coordenadas (1, 0) e o ponto D tem coordenadas (-1, 0), como na figura abaixo.
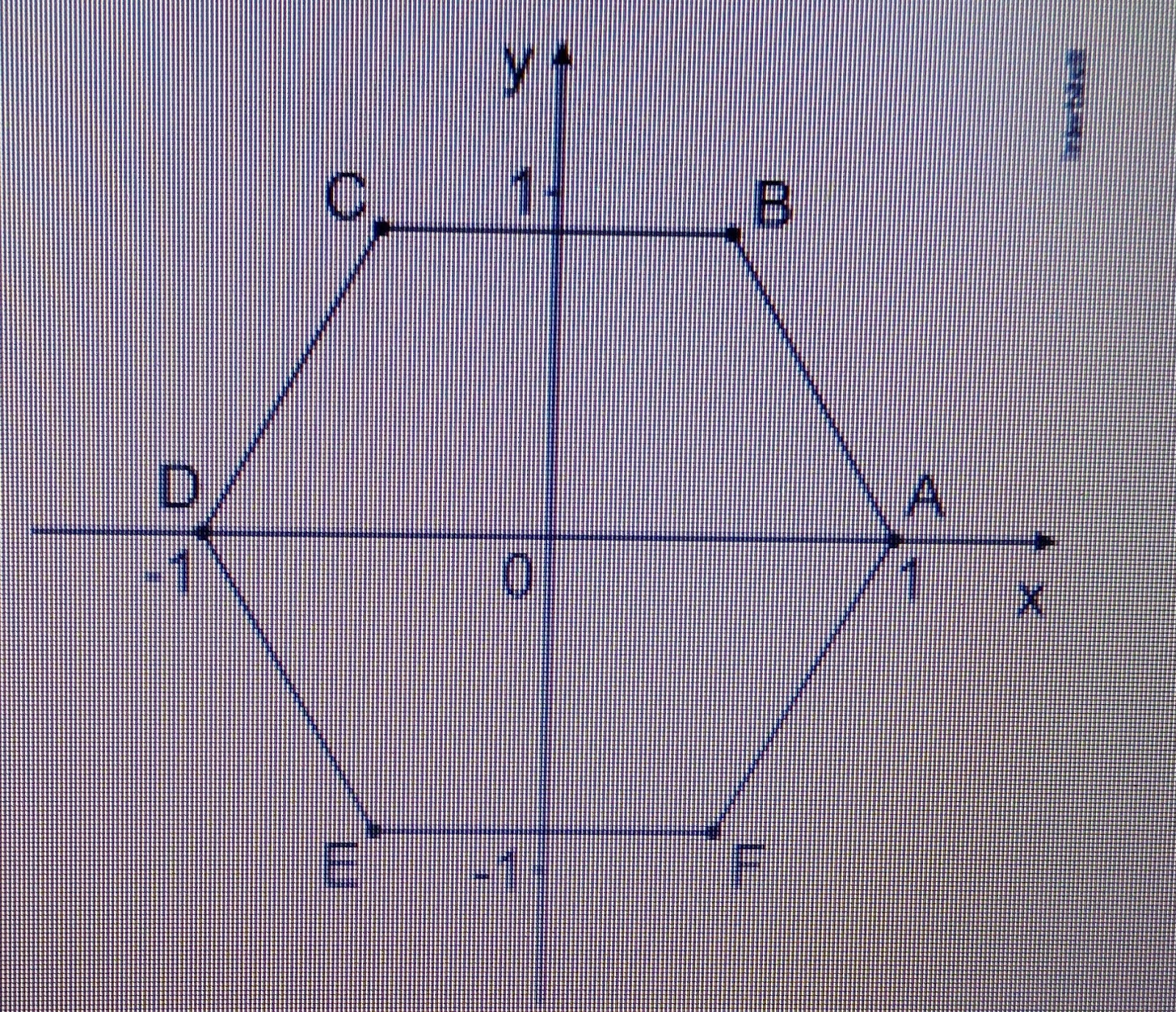
A equação da reta que passa pelos pontos B e D é :
R:
y = √3x/3 + √3/3
Eu queria saber se tem como resolver essa questão, pela Equação Segmentaria da Reta ?
Dessa forma,
x/p + y/q = 1
p= -1
q= (sqrt(3)/2) O ponto do y do B, eu achei fazendo a altura do triângulo equilátero.
x/-1 + y/(sqrt(3)/2) =1
Só que pra mim dá :
y= (sqrt(3)/(2))x + (sqrt(3)/2)
:scratch:
:scratch:
A equação da reta que passa pelos pontos B e D é :
R:
y = √3x/3 + √3/3
Eu queria saber se tem como resolver essa questão, pela Equação Segmentaria da Reta ?
Dessa forma,
x/p + y/q = 1
p= -1
q= (sqrt(3)/2) O ponto do y do B, eu achei fazendo a altura do triângulo equilátero.
x/-1 + y/(sqrt(3)/2) =1
Só que pra mim dá :
y= (sqrt(3)/(2))x + (sqrt(3)/2)
:scratch:
:scratch:
Luana Skywalker- Jedi
- Mensagens : 338
Data de inscrição : 08/09/2009
Localização : Condado (Florianópolis - SC)
Re: Equação Segmentária da Reta
por Elcioschin Sex 01 Dez 2017, 17:42
OAB é equilátero ---> OA = OB = AB = 1 ---> xB= 1/2 ---> yB = √3/2
Ponto D ---> D(-1, 0)
Coeficiente angular da reta BD: m = (YB - yD)/(xB - xD) ---> m = (√3/2 - 0)/(1/2 + 1) ---> m = √3/3
y - yD = m.(x - xD) ---> y - 0 = (√3/3).(x + 1) ---> y = (√3/3).x + √3/3
Ponto D ---> D(-1, 0)
Coeficiente angular da reta BD: m = (YB - yD)/(xB - xD) ---> m = (√3/2 - 0)/(1/2 + 1) ---> m = √3/3
y - yD = m.(x - xD) ---> y - 0 = (√3/3).(x + 1) ---> y = (√3/3).x + √3/3
Elcioschin- Grande Mestre
- Mensagens : 73160
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Luana Skywalker- Jedi
- Mensagens : 338
Data de inscrição : 08/09/2009
Localização : Condado (Florianópolis - SC)
Tópicos semelhantes» Equação segmentária da Reta, dúvida.
» equação segmentária da reta AB
» Equação segmentária da reta
» Equação segmentária da reta
» Equação Segmentária da Reta
» equação segmentária da reta AB
» Equação segmentária da reta
» Equação segmentária da reta
» Equação Segmentária da Reta
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
