tg x = cotg x
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
tg x = cotg x
por Mathematicien Sáb 01 Jul 2017, 19:25
Boa noite!
Eu fiz o gráfico de tg(x) e cotg(x) e vi que se entrelaçam em alguns pontos.
Daí tentei fazer tg x = cotg x para saber que pontos são esses.
tg x = 1 / tg x
tg²x = 1
tg²x = tg(pi/4 + k.pi)
E agora, como continuo?
Obrigado
Eu fiz o gráfico de tg(x) e cotg(x) e vi que se entrelaçam em alguns pontos.
Daí tentei fazer tg x = cotg x para saber que pontos são esses.
tg x = 1 / tg x
tg²x = 1
tg²x = tg(pi/4 + k.pi)
E agora, como continuo?
Obrigado
Mathematicien- Mestre Jedi
- Mensagens : 668
Data de inscrição : 14/08/2014
Re: tg x = cotg x
por Victor011 Sáb 01 Jul 2017, 19:39
Veja:
tg x=cotg x\iff tg x=\frac{1}{tg x}\iff tg^2 x=1
Como tg x é um número real, teremos dois casos: tg x=1 ou tg x=-1.
Analisando o primeiro caso:
tg x=1\iff x=\frac{\pi}{4}+k\pi\;\;\;com\;k\in \mathbb{Z}
Analisando o segundo caso:
tg x=-1\iff x=\frac{3\pi}{4}+k\pi\;\;\;com\;k\in \mathbb{Z}
Fazendo a união dos resultados encontrados:
\boxed{S=\{x\in\Re/\;x=\frac{\pi}{4}+\frac{k\pi}{2},\;com\;k\in \mathbb{Z}\}}
Como tg x é um número real, teremos dois casos: tg x=1 ou tg x=-1.
Analisando o primeiro caso:
Analisando o segundo caso:
Fazendo a união dos resultados encontrados:
Victor011- Fera
- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Re: tg x = cotg x
por Mathematicien Sáb 01 Jul 2017, 21:24
Victor, eu acho que entendi, mas ainda me sinto inseguro. Pode me explicar mais detalhadamente a parte da união dos resultados encontrados? Como as duas últimas equações se tornam essa solução geral?
Mathematicien- Mestre Jedi
- Mensagens : 668
Data de inscrição : 14/08/2014
Re: tg x = cotg x
por Victor011 Sáb 01 Jul 2017, 22:04
primeiro caso:{...,-3π/4, π/4, 5π/4,...}
Segundo caso:{...,-π/4, 3π/4, 7π/4,...}
União dos casos:{...,-3π/4, -π/4, π/4, 3π/4, 5π/4, 7π/4,...}
Note que os resultados da união "pulam" de π/2 em π/2, por isso o +kπ/2 na resposta. Eu escrevi dessa forma só para ficar mais bonito, mas poderia ter deixado a resposta da seguinte forma: (o símbolo "V" significa "ou")
S\{x\in\Re/x=\frac{\pi}{4}+k\pi\vee x=\frac{3\pi}{4}+k\pi,\;com\;k\in \mathbb{Z}\}
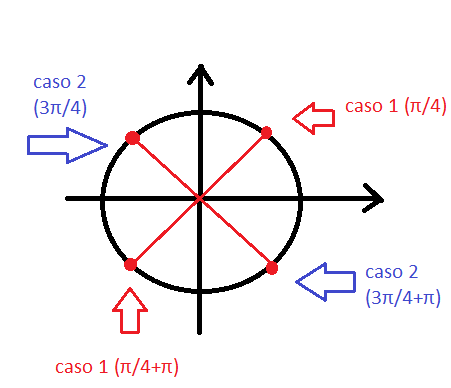
É possível ver pelo círculo trigonométrico também. Note que as soluções do caso 1, por exemplo, nada mais são do que pegar o π/4 e ficar dando meia volta no círculo. Veja:
Segundo caso:{...,-π/4, 3π/4, 7π/4,...}
União dos casos:{...,-3π/4, -π/4, π/4, 3π/4, 5π/4, 7π/4,...}
Note que os resultados da união "pulam" de π/2 em π/2, por isso o +kπ/2 na resposta. Eu escrevi dessa forma só para ficar mais bonito, mas poderia ter deixado a resposta da seguinte forma: (o símbolo "V" significa "ou")
É possível ver pelo círculo trigonométrico também. Note que as soluções do caso 1, por exemplo, nada mais são do que pegar o π/4 e ficar dando meia volta no círculo. Veja:
Victor011- Fera
- Mensagens : 663
Data de inscrição : 21/10/2015
Idade : 26
Localização : Rio de Janeiro, Brasil
Re: tg x = cotg x
por Mathematicien Sáb 01 Jul 2017, 22:12
Agora entendi perfeitamente!! Obrigado, Victor!!
Mathematicien- Mestre Jedi
- Mensagens : 668
Data de inscrição : 14/08/2014
Tópicos semelhantes» cotg x . cos x
» Sec, cossec e cotg
» Determine cotg
» A (cotg x + tg x)² é igual a:
» O valor de (tg 10º + cotg 10º)sen 20º é:
» Sec, cossec e cotg
» Determine cotg
» A (cotg x + tg x)² é igual a:
» O valor de (tg 10º + cotg 10º)sen 20º é:
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
