(AFA- Epcar)

Na cidade de Macapá, no Amapá, Fernando envia uma mensagem via satélite para Maria na mesma cidade.
A mensagem é intermediada por um satélite geoestacionário, em órbita circular cujo centro coincide com o centro geométrico da Terra, e por uma operadora local de telecomunicação da seguinte forma: o sinal de informação parte do celular de Fernando direto para o satélite que instantaneamente retransmite para a operadora, que, da mesma forma, transmite para o satélite mais uma vez e, por fim, é retransmitido para o celular de Maria.
Considere que esse sinal percorra todo trajeto em linha reta e na velocidade da luz, c; que as dimensões da cidade sejam desprezíveis em relação à distância que separa o satélite da Terra, que este satélite esteja alinhado perpendicularmente à cidade que se encontra ao nível do mar e na linha do equador. Sendo, M, massa da Terra, T, período de rotação da Terra, RT , raio da Terra e G, a constante de gravitação universal, o intervalo de tempo entre a emissão do sinal no celular de Fernando e a recepção no celular de Maria, em função de c, M, T, G e RT é  :
GAB : 4/c [ ∛  (T² GM/ 4 ∏²) - RT ]

As dimensões da cidade são desprezíveis em relação à distância entre o satélite e a superfície, logo o tempo gasto pelo sinal nesse percurso também é desprezível.

Para descobrir o tempo gasto, primeiro precisamos da distância entre o satélite e a superfície. Como o raio da órbita do satélite não é dado, vamos calcular através da força centrípeta (lembrando que o satélite é geoestacionário, ou seja, tem período de rotação igual ao da Terra):



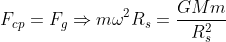
[img]https://latex.codecogs.com/gif.latex?\Rightarrow&space;R_s&space;=&space;\sqrt[3]{\frac{T^2GM}{4\pi^2}}[/img]

A distância, é, portanto:
[img]https://latex.codecogs.com/gif.latex?d&space;=&space;R_s&space;-&space;R_T&space;\Rightarrow&space;d&space;=&space;\sqrt[3]{\frac{T^2GM}{4\pi^2}}&space;-&space;R_T[/img]

Assim:
[img]https://latex.codecogs.com/gif.latex?\Delta&space;t&space;=&space;\frac{d}{v}&space;\Rightarrow&space;\Delta&space;t&space;=&space;\frac{1}{c}&space;\cdot&space;\left[&space;\sqrt[3]{\frac{T^2GM}{4\pi^2}}&space;-&space;R_T&space;\right&space;][/img]

Essa distância é percorrida quatro vezes: do celular de Fernando ao satélite, do satélite à operadora, da operadora ao satélite e do satélite ao celular de Maria. A resposta é:

[img]https://latex.codecogs.com/gif.latex?\Delta&space;t&space;=&space;\frac{4}{c}&space;\cdot&space;\left[&space;\sqrt[3]{\frac{T^2GM}{4\pi^2}}&space;-&space;R_T&space;\right&space;][/img].

Edit: o latex ficou zuado, na janela de edição tá normal... estranho.