Combinações Simples
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
 Combinações Simples
Combinações Simples
Essa é uma dissertação-explicação sobre a dedução da fórmula das combinações simples. É um texto extenso em que procurei concatenar minuciosamente essa análise, já que quando buscava pela teoria em diversas fontes, ainda tinha muita, muita dificuldade mesmo para compreender. Agora, no entanto, creio que da forma que tentarei expor não haverá espaço para dúvidas.
A combinação simples é a quantidade de grupos (subconjuntos) com k elementos distintos entre n elementos distintos dados. Onde o que difere estes agrupamentos entre si é a natureza dos elementos que encerram, e não a sua ordem! Esta é geralmente indicada por:
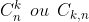
Por exemplo, dado o conjunto A={a,b,c}, quantos grupos de dois elementos distintos podemos formar?
Evidentemente, estes devem ser os subconjuntos {a;b}, {a;c} , {b;c} .
Salientemos, ainda, que os subconjuntos {b;a}, {c;a} , {c;b} são idênticos aos subconjuntos anteriores, pois a natureza dos elementos deste é a mesma que a daqueles, a diferença é que a ordem está trocada. Ocasião esta em que ab=ba.
Para efeito de explicação da expressão de uma combinação, vamos analisar o caso em que é preciso fazer uma combinação de 3 elementos distintos entre 5 elementos distintos dados a,b,c,d,e. Frisando que esta é uma só maneira de analisar inicialmente as combinações simples.
As combinações simples, em que todas contêm elementos distintos, são exatamente:
{a,b,c} {a,b,d} {a,b,e} {b,c,d} {b,c,e}
{c,d,e} {a,c,d} {a,d,e} {a,c,e} {b,d,e} ∴ C3,5=10
Do Princípio Fundamental da Contagem, poderíamos ser induzidos a pensar que, sendo as escolhas a serem feitas: a do primeiro elemento, a do segundo elemento e a do terceiro elemento. Sendo ainda estes distintos, as maneiras de contar essas combinações seriam:
A resposta parece ser igual a 60 modos que agrupar 3 elementos diferentes.
Realmente esta maneira de contar garante que em um mesmo grupo não haverá elementos iguais entre si dentro de cada grupo contado. Todavia foram contados, ainda, agrupamentos repetidos com os mesmos elementos, mas em ordens trocadas.
Este método conta, por exemplo, o primeiro grupo {a;b;c}, que corretamente contém todos elementos distintos entre si como especificamos, mas conta também a existência dos outros grupos com elementos distintos entre si
{a;c;b}, {b;a;c}, {b;c;a}, {c;a;b} e {c;b;a}.
Ao total, foram contados 6 grupos que contêm os elementos a,b e c, vistos acima. Ora, se estes possuem uma mesma natureza, são com certeza iguais do ponto de vista de uma combinação simples. Daí, estão contados:
{a;b;c}, {a;c;b}, {b;a;c}, {b;c;a}, {c;a;b} , {c;b;a} = {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c} = 6{a;b;c}
Portanto veja que o que deveria ser um único agrupamento, fora contado 6 vezes.
O mesmo ocorre para os outros 9 grupos que vimos acima. Todos são contados 6 vezes. De modo que em nossa contagem, o que acontece é:
6{a,b,c} + 6{a,b,d} + 6{a,b,e} + 6{b,c,d} + 6{b,c,e} + 6{c,d,e} + 6{a,c,d} + 6{a,d,e} + 6{a,c,e} + 6{b,d,e} = 60
ou seja:
6[{a,b,c} {a,b,d} {a,b,e} {b,c,d} {b,c,e} {c,d,e} {a,c,d} {a,d,e} {a,c,e} {b,d,e}]=60
Para encontrar o número de agrupamentos desta combinação simples, dividimos o resultado encontrado na primeira resposta pelo número de vezes em que aparecem repetidos, isto é, 60÷6= 10.
Mas como saber quantas vezes cada grupo de 3 elementos fora contado? Ora, o número de repetições é o mesmo número de permutações possíveis dentro de um agrupamento, neste caso, o número de permutações possíveis entre 3 elementos de um agrupamento é dado por P3 = 3! = 6, oque confere com o número de grupos contados.
Resumindo, contam-se todas as possíveis relações distintas segundo o princípio fundamental da contagem (5×4×3 = 60 modos) e o divide-se pelo número de repetições dada por P3=6.
_______________________________________________________
Segundo exemplo: Combinações de 4 elementos distintos entre 7 elementos distintos dados (C4,7)
Do Princípio Fundamental da Contagem, vem:
Mas houve um número de repetições, de cada grupo de 4 elementos, igual ao número de permutações possíveis estre estes 4 elementos, dado por P4 = 4! = 24 repetições.
Dividindo-se o resultado encontrado pelo número de vezes em que contamos repetições vem: 840 ÷ 24 = 35 maneiras.
________________________________________________________
Generalizando:
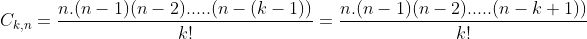
E se multiplicarmos o numerador e o denominador da fração por (n-k)! vem:
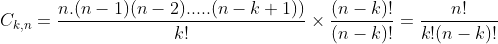
Finalmente: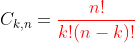
A combinação simples é a quantidade de grupos (subconjuntos) com k elementos distintos entre n elementos distintos dados. Onde o que difere estes agrupamentos entre si é a natureza dos elementos que encerram, e não a sua ordem! Esta é geralmente indicada por:
Por exemplo, dado o conjunto A={a,b,c}, quantos grupos de dois elementos distintos podemos formar?
Evidentemente, estes devem ser os subconjuntos {a;b}, {a;c} , {b;c} .
Salientemos, ainda, que os subconjuntos {b;a}, {c;a} , {c;b} são idênticos aos subconjuntos anteriores, pois a natureza dos elementos deste é a mesma que a daqueles, a diferença é que a ordem está trocada. Ocasião esta em que ab=ba.
Para efeito de explicação da expressão de uma combinação, vamos analisar o caso em que é preciso fazer uma combinação de 3 elementos distintos entre 5 elementos distintos dados a,b,c,d,e. Frisando que esta é uma só maneira de analisar inicialmente as combinações simples.
As combinações simples, em que todas contêm elementos distintos, são exatamente:
{a,b,c} {a,b,d} {a,b,e} {b,c,d} {b,c,e}
{c,d,e} {a,c,d} {a,d,e} {a,c,e} {b,d,e} ∴ C3,5=10
Do Princípio Fundamental da Contagem, poderíamos ser induzidos a pensar que, sendo as escolhas a serem feitas: a do primeiro elemento, a do segundo elemento e a do terceiro elemento. Sendo ainda estes distintos, as maneiras de contar essas combinações seriam:
| 1º elemento | 2º elemento | 3º elemento | Contagem |
| 5 maneiras | 4 maneiras | 3 maneiras | 5×4×3 = 60 modos |
A resposta parece ser igual a 60 modos que agrupar 3 elementos diferentes.
Realmente esta maneira de contar garante que em um mesmo grupo não haverá elementos iguais entre si dentro de cada grupo contado. Todavia foram contados, ainda, agrupamentos repetidos com os mesmos elementos, mas em ordens trocadas.
Este método conta, por exemplo, o primeiro grupo {a;b;c}, que corretamente contém todos elementos distintos entre si como especificamos, mas conta também a existência dos outros grupos com elementos distintos entre si
{a;c;b}, {b;a;c}, {b;c;a}, {c;a;b} e {c;b;a}.
Ao total, foram contados 6 grupos que contêm os elementos a,b e c, vistos acima. Ora, se estes possuem uma mesma natureza, são com certeza iguais do ponto de vista de uma combinação simples. Daí, estão contados:
{a;b;c}, {a;c;b}, {b;a;c}, {b;c;a}, {c;a;b} , {c;b;a} = {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c}, {a;b;c} = 6{a;b;c}
Portanto veja que o que deveria ser um único agrupamento, fora contado 6 vezes.
O mesmo ocorre para os outros 9 grupos que vimos acima. Todos são contados 6 vezes. De modo que em nossa contagem, o que acontece é:
6{a,b,c} + 6{a,b,d} + 6{a,b,e} + 6{b,c,d} + 6{b,c,e} + 6{c,d,e} + 6{a,c,d} + 6{a,d,e} + 6{a,c,e} + 6{b,d,e} = 60
ou seja:
6[{a,b,c} {a,b,d} {a,b,e} {b,c,d} {b,c,e} {c,d,e} {a,c,d} {a,d,e} {a,c,e} {b,d,e}]=60
Para encontrar o número de agrupamentos desta combinação simples, dividimos o resultado encontrado na primeira resposta pelo número de vezes em que aparecem repetidos, isto é, 60÷6= 10.
Mas como saber quantas vezes cada grupo de 3 elementos fora contado? Ora, o número de repetições é o mesmo número de permutações possíveis dentro de um agrupamento, neste caso, o número de permutações possíveis entre 3 elementos de um agrupamento é dado por P3 = 3! = 6, oque confere com o número de grupos contados.
Resumindo, contam-se todas as possíveis relações distintas segundo o princípio fundamental da contagem (5×4×3 = 60 modos) e o divide-se pelo número de repetições dada por P3=6.
_______________________________________________________
Segundo exemplo: Combinações de 4 elementos distintos entre 7 elementos distintos dados (C4,7)
Do Princípio Fundamental da Contagem, vem:
| 1ºelemento | 2ºelemento | 3ºelemento | 4ºelemento | Contagem |
| 7 maneiras | 6 maneiras | 5 maneiras | 4 maneiras | 7×6×5×4=840 maneiras |
Mas houve um número de repetições, de cada grupo de 4 elementos, igual ao número de permutações possíveis estre estes 4 elementos, dado por P4 = 4! = 24 repetições.
Dividindo-se o resultado encontrado pelo número de vezes em que contamos repetições vem: 840 ÷ 24 = 35 maneiras.
________________________________________________________
Generalizando:
E se multiplicarmos o numerador e o denominador da fração por (n-k)! vem:
Finalmente:

Smasher- Mestre Jedi

- Mensagens : 583
Data de inscrição : 20/03/2015
Idade : 27
Localização : São Paulo, SP, Brasil
 Tópicos semelhantes
Tópicos semelhantes» Combinações Simples
» combinações simples
» Combinações simples-questão
» Arranjos e combinações simples NM4
» Combinações simples - (comissão de alunos)
» combinações simples
» Combinações simples-questão
» Arranjos e combinações simples NM4
» Combinações simples - (comissão de alunos)
PiR2 :: Recursos extras :: Demonstrações
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|













