Problema do IME -66 de Geometria Espacial
4 participantes
Página 1 de 1
Problema do IME -66 de Geometria Espacial
por gabriel.dutra Dom 07 Fev 2016, 18:09
Olá, tudo bem?
Gostaria de deixar um problema que está me parecendo bastante estranho quanto ao gabarito.
(IME-66) Um cilindro é circunscrito a uma esfera de raio R. Um cone é circunscrito a esse cilindro de modo que sua altura seja 4R. Calcular a relação entre a área lateral do cone e aq área da esfera.
A resposta no gabarito é sqrt 5, porém quando eu fiz deu como resposta sqrt5/pi. Como procedo?
Desde já, agradeço a compreensão.
Gostaria de deixar um problema que está me parecendo bastante estranho quanto ao gabarito.
(IME-66) Um cilindro é circunscrito a uma esfera de raio R. Um cone é circunscrito a esse cilindro de modo que sua altura seja 4R. Calcular a relação entre a área lateral do cone e aq área da esfera.
A resposta no gabarito é sqrt 5, porém quando eu fiz deu como resposta sqrt5/pi. Como procedo?
Desde já, agradeço a compreensão.
gabriel.dutra- Iniciante
- Mensagens : 26
Data de inscrição : 15/02/2014
Idade : 27
Localização : Hortolandia -SP
Re: Problema do IME -66 de Geometria Espacial
por Euclides Dom 07 Fev 2016, 19:05
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
gabriel.dutra- Iniciante
- Mensagens : 26
Data de inscrição : 15/02/2014
Idade : 27
Localização : Hortolandia -SP
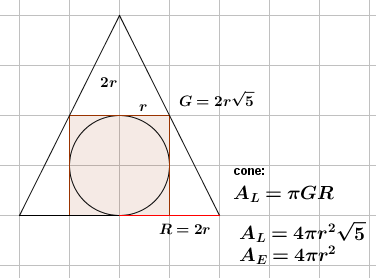
porque G=2r√5 sendo h=4r e R=2r, 4r^2+16r^2=4r√5
por lovesi Seg 06 Jun 2022, 02:37
Euclides escreveu:
lovesi- Iniciante
- Mensagens : 1
Data de inscrição : 06/06/2022
Re: Problema do IME -66 de Geometria Espacial
por petras Seg 06 Jun 2022, 10:48
???
[latex]G^2 = 4r^2+16r^2=20r^2\\ G = \sqrt{20r^2}=2r\sqrt5[/latex]
[latex]G^2 = 4r^2+16r^2=20r^2\\ G = \sqrt{20r^2}=2r\sqrt5[/latex]
____________________________________________
_______________________________
"Ex nihilo nihil fit"
petras- Monitor
- Mensagens : 2117
Data de inscrição : 10/06/2016
Idade : 59
Localização : bragança, sp, brasil
Tópicos semelhantes» problema de geometria espacial
» Geometria espacial - volume
» [Nv: Médio] Problema de Geometria Plana e Espacial
» Geometria Espacial
» Geometria ESPACIAL
» Geometria espacial - volume
» [Nv: Médio] Problema de Geometria Plana e Espacial
» Geometria Espacial
» Geometria ESPACIAL
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
