(Ufmg 95) Geometria Plana

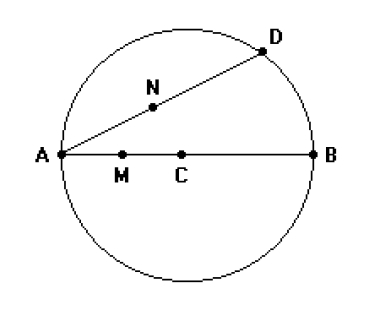
(Ufmg 95) Observe a figura seguir. Nessa figura, D é um ponto da circunferência de centro C e diâmetro AB, e M e N são pontos médios dos segmentos AC e AD, respectivamente. A medida MN em função do diâmetro AB é:

a) (AB)/5
b) (2/5) AB
c) (AB)/4
d) (AB)/3
e) (AB)/2

Spoiler:

Como eu poderia afirmar que MN é paralelo a CD? Valeu gente

GrunsGruns escreveu:Como eu poderia afirmar que MN é paralelo a CD? Valeu gente

O enunciado garante que M e N são pontos médios.
Partindo disto, você pode afirmar aquele paralelismo aplicando o teorema de Tales ao inverso.

Alguém poderia fazer a resolução dessa questão? Mesmo sabendo que MN e CD são paralelos não consegui desenvolver os cálculos

Maiara,
a figura não existe mais e também não lembro como fiz da "vespa-assada" mas deve ser algo parecido com isto.

(sinto, tinha preparado uma figura mas o botão do fórum que as insere está com falha: "ERROR: Cannot obtain db informations 2". Tentarei novamente depois).

Vou tentar descrever.

trace DB, está formado o triângulo retângulo ADB, pois que inscrito numa semicircunferência.
C é ponto médio da hipotenusa, portanto AC = CB = CD = r.
M e N são pontos médios, portanto AM = MC = r/2 e AN = ND = k.
AB e AD são concorrentes e AM/AN = MC/ND ---->  (r/2)/k = (r/2)/k; portanto, por Tales, MN // CD.
∆AMN ~ ∆ACD  ----->  MN/CD = AN/AC  ----->  MN/r = (r/2)/r  ----->  MN = r/2 .............(1)
AB = 2.r  ----->  r = AB/2 ...............(2)
(2) em (1): MN = AB/4

agora de manhã consegui inserir a figura.