Equação da Esfera - Geometria Analítica
2 participantes
Página 1 de 1
Equação da Esfera - Geometria Analítica
por Pietro di Bernadone Sex 17 Abr 2015, 18:55
Sejam os planos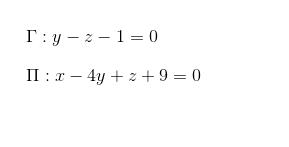 
e a reta 
da equação 
. Escreva a equação da
esfera com centro sobre e que seja tangente aos planos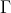 
e 
.
. E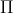screva a equação da esfera com centro sobre
Pietro di Bernadone- Grupo
Velhos amigos do Fórum
- Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Equação da Esfera - Geometria Analítica
por mauk03 Ter 21 Abr 2015, 08:25
Se o centro C da esfera está sobre a reta r, então:
C = (1 - λ, -3 + λ, 2 + 2λ)
Se a esfera é tangente aos planos Γ e Π, então a distância entre C e Γ deve ser igual a distância entre C e Π.
Sendo:
d(C,Γ) = |0*(1 - λ) + 1*(-3 + λ) - 1*(2 + 2λ) - 1|/√(0² + 1² + (-1)²) = |-λ - 6|/√2 = |λ + 6|/√2
d(C,Π) = |1*(1 - λ) - 4*(-3 + λ) + 1*(2 + 2λ) + 9|/√(1² + (-4)² + 1²) = 3|-λ + 8|/√18 = |λ - 8|/√2
Então devemos ter:
|λ + 6|/√2 = |λ - 8|/√2 --> λ = 1
Para λ = 1:
C = (1 - 1, -3 + 1, 2 + 2*1) = (0, -2, 4)
Raio = d(C,Γ) = |1 + 6|/√2 = 7/√2
Portanto, a equação da esfera é x² + (y + 2)² + (z - 4)² = (7/√2)².
C = (1 - λ, -3 + λ, 2 + 2λ)
Se a esfera é tangente aos planos Γ e Π, então a distância entre C e Γ deve ser igual a distância entre C e Π.
Sendo:
d(C,Γ) = |0*(1 - λ) + 1*(-3 + λ) - 1*(2 + 2λ) - 1|/√(0² + 1² + (-1)²) = |-λ - 6|/√2 = |λ + 6|/√2
d(C,Π) = |1*(1 - λ) - 4*(-3 + λ) + 1*(2 + 2λ) + 9|/√(1² + (-4)² + 1²) = 3|-λ + 8|/√18 = |λ - 8|/√2
Então devemos ter:
|λ + 6|/√2 = |λ - 8|/√2 --> λ = 1
Para λ = 1:
C = (1 - 1, -3 + 1, 2 + 2*1) = (0, -2, 4)
Raio = d(C,Γ) = |1 + 6|/√2 = 7/√2
Portanto, a equação da esfera é x² + (y + 2)² + (z - 4)² = (7/√2)².
mauk03- Fera
- Mensagens : 831
Data de inscrição : 14/04/2012
Idade : 31
Localização : TB - Paraná - Br
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
