Comprimento

por Anner Qua 04 Mar 2015, 14:39

Na figura abaixo, determine o comprimento da corrente que envolve as duas rodas, sabendo que o raio da roda menor mede 2cm e o raio da roda maior, 4 cm, e a distância entre os centros das duas rodas mede 12 cm.

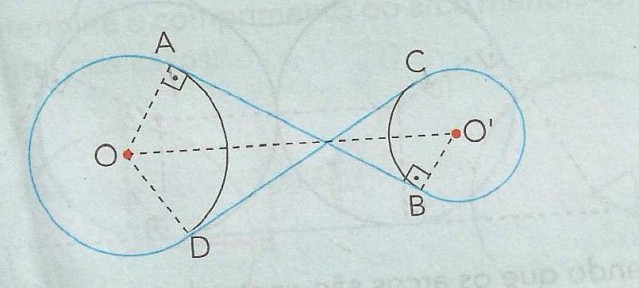
Comprimento Hv1841

Spoiler:

Tentei fazer:

1) sendo o triângulo retângulo com ângulos de 90º, 30º e 60º, apliquei o sen

para a circunferência de r= 4--> sen 60º=x/4---> V3/2=x/4-->2V3 como são dois triângulos, 4V3.

para a circunferência de r= 2--> sen 60º=x/2---> V3/2=x/2-->V3 como são dois triângulos, 2V3.

2) apliquei a fórmula do comprimento(C=2.pi.r) resultando em 8pi e 4pi

3) 12pi - 6V3--> 3(4pi- 2V3)

por **Medeiros** Qui 05 Mar 2015, 03:05

Você acertou que os ângulos são de 60°. Então temos:
arcos menores -----> BC = AD = 120° = 2pi/3
arcos maiores -----> BC = AD = 240° = 4pi/3
comprimento dos arcos maiores -----> L' = 2×4pi/3 + 4×4pi/3 = 8pi

comprimento das tangentes -----> L" = 2×6.V3 = 12.V3

comprimento da correia -----> L = L' + L" ----> L = 4 (3.V3 + 2pi) cm

por vscarv Seg 09 Mar 2015, 11:04

Medeiros,
Será que poderia fazer assim?

Sen 60=x/8
Sendo a hipotenusa da roda maior =8

X=4V3 como são triângulos 8V3

Sen 60=y/4
Sendo y a hipotenusa da roda menor =4
Y=2V3 como são dois triângulos 4V3

Somando dá 12V3.

A minha única dúvida é quanto considerar a hipotenusa como o dobro de cada raio. O que você acha?

por Conteúdo patrocinado

Comprimento

Comprimento

Re: Comprimento

Re: Comprimento

Re: Comprimento

Um fórum livre e democrático.