(EN) "Area Hachurada"
2 participantes
Página 1 de 1
(EN) "Area Hachurada"
por boris benjamim de paula Seg 23 Ago 2010, 10:56
Na figura 
é um triângulo equilátero de lado 
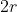e 
,
são arcos de circunferencia de raio 
.Os segmentos 
são perpendiculares 
é uma semicircunferencia de centro em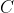 
.se 
e a soma das áreas hachuradas vale r^2+\frac{5}{9} "\large (\sqrt{3}-\frac{\pi}{2})r^2+\frac{5}{9}")
então o valor de 
é:
2^\frac{-1}{2}\\\\(b)2^\frac{-1}{4}\\\\(c)2^\frac{1}{4}\\\\(d)2^\frac{1}{2}\\\\(e)2 "\large (a)2^\frac{-1}{2}\\\\(b)2^\frac{-1}{4}\\\\(c)2^\frac{1}{4}\\\\(d)2^\frac{1}{2}\\\\(e)2")
obs: eu só não consegui encontrar MN
obs: eu só não consegui encontrar MN
boris benjamim de paula- Grupo
Velhos amigos do Fórum
- Mensagens : 505
Data de inscrição : 19/01/2010
Idade : 34
Localização : natal
Re: (EN) "Area Hachurada"
por Elcioschin Seg 23 Ago 2010, 12:12
Área do "biquini cavadão" PQR:
S = (2r)²*V3/4 - 3*(pi*r²/6) ----> S = (V3 - pi/2)*r²
Por M trace uma perpendicular a CS. Seja T o pé da perpendicular.
NS = MT ----> NS = CM*sena ----> NS = r*2*V2/3
sena = 2*V2/3 ----> sen²a = 8/9 ----> cos²a = 1/9 ----> cosa = 1/3
CT = CM*cosa ----> CT = r*1/3 ----> CT = r/3
MN = TS ----> MN = CS - CT ----> MN = r - r/3 ----> MN = 2r/3
Área do trapézio MNSC ----> S' = (CS + MN)*NS/2
S' = (r + 2r/3)*(r*2*V2/3)/2 ----> S' = (5*V2/9)*r²
S + S' = (V3 - pi/2)*r² + (5*V2/9)*r²
Acho que seu enunciado está errado quanto á soma das áreas hachuradas:
Deve ser ..... (5/*V2)*r² ao invés de 5/9
Se assim for ----> r = 1
S = (2r)²*V3/4 - 3*(pi*r²/6) ----> S = (V3 - pi/2)*r²
Por M trace uma perpendicular a CS. Seja T o pé da perpendicular.
NS = MT ----> NS = CM*sena ----> NS = r*2*V2/3
sena = 2*V2/3 ----> sen²a = 8/9 ----> cos²a = 1/9 ----> cosa = 1/3
CT = CM*cosa ----> CT = r*1/3 ----> CT = r/3
MN = TS ----> MN = CS - CT ----> MN = r - r/3 ----> MN = 2r/3
Área do trapézio MNSC ----> S' = (CS + MN)*NS/2
S' = (r + 2r/3)*(r*2*V2/3)/2 ----> S' = (5*V2/9)*r²
S + S' = (V3 - pi/2)*r² + (5*V2/9)*r²
Acho que seu enunciado está errado quanto á soma das áreas hachuradas:
Deve ser ..... (5/*V2)*r² ao invés de 5/9
Se assim for ----> r = 1
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
resposta
por boris benjamim de paula Seg 23 Ago 2010, 12:29
dessa vez da certo msm, é 5\9 .
elcio se eu fizer o triângulo CNS o ângulo alpha não fica alpha\2?
elcio se eu fizer o triângulo CNS o ângulo alpha não fica alpha\2?
boris benjamim de paula- Grupo
Velhos amigos do Fórum - Mensagens : 505
Data de inscrição : 19/01/2010
Idade : 34
Localização : natal
Re: (EN) "Area Hachurada"
por Elcioschin Seg 23 Ago 2010, 12:39
Neste caso temos:
(5*V2/9)*r² = 5/9
V2*r² = 1
[2^(1/2)]*r² = 1
r² = 1/2^(1/2)
r² = 2^(-1/2)
r = 2^(-1/4) ----> Alternativa B
(5*V2/9)*r² = 5/9
V2*r² = 1
[2^(1/2)]*r² = 1
r² = 1/2^(1/2)
r² = 2^(-1/2)
r = 2^(-1/4) ----> Alternativa B
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
