Geometria espacial - CUBO

Eu gostaria de uma outra opinião sobre este exercício , se há algum modo menos extenso para a resolução , já que o meu , levando em consideração todas as contas , ficou muito comprido . 

- Qual a distância entre um vértice de um cubo, com aresta medindo 20 raiz de 6 , e uma das diagonais do cubo que não passam por esse vértice. 


Resolvi desse jeito , marcado em vermelho, logo abaixo : 

1 teorema de Pitágoras para a diagonal da face do cubo 
2 Outro teorema de Pitágoras para o cálculo da diagonal do cubo
3 Dividi a diagonal d do cubo em d - x e x e fiz um teorema de Pitágoras para cada parte 
4 igualei os dois teoremas ( que resultavam na distancia pedida do exercício )
e deu a resposta , depois de 15 minutos ...

Há outro método ? qual ? A resposta é 40 . 

Agradeço a atenção 

giuseppebrandi escreveu:Eu gostaria de uma outra opinião sobre este exercício , se há algum modo menos extenso para a resolução , já que o meu , levando em consideração todas as contas , ficou muito comprido . 

- Qual a distância entre um vértice de um cubo, com aresta medindo 20 raiz de 6 , e uma das diagonais do cubo que não passam por esse vértice. 


Resolvi desse jeito , marcado em vermelho, logo abaixo : 

1 teorema de Pitágoras para a diagonal da face do cubo 
2 Outro teorema de Pitágoras para o cálculo da diagonal do cubo
3 Dividi a diagonal d do cubo em d - x e x e fiz um teorema de Pitágoras para cada parte 
4 igualei os dois teoremas ( que resultavam na distancia pedida do exercício )
e deu a resposta , depois de 15 minutos ...

Há outro método ? qual ? A resposta é 40 . 

Agradeço a atenção 

Boa tarde, Giuseppe.

Identificando com letras os 8 vértices do cubo, vem:
Face frontal:
A = vértice inferior esquerdo
B = vértice superior esquerdo
C = vértice superior direito
D = vértice inferior direito

Face do fundo:
E = vértice inferior esquerdo (olhando da frente para o fundo)
F = vértice superior esquerdo
G = vértice superior direito
H = vértice inferior direito

Tomando por base o vértice A, procurei determinar a distância (d) desde A até a diagonal BH.

Cálculo da diagonal da face inferior (AEHD):
AH = 20√6*√2 = 20√12 = 20*2√3 = 40√3

Cálculo da diagonal BH do cubo:
√[3*(20√6)²] = √(3*2400) = √7200 = 60√2

Assim, a aresta vertical AB com a diagonal AH da face inferior e a diagonal BH do cubo formam um triângulo retângulo em A.
Logo, a distância desejada (d) é igual à altura da hipotenusa BH.
AB * AH = d * BH
d = AB*AH/BH
d = 20√6*40√3/(60√2)
d = 800√18/(60√2)
d = 800*3√2/(60√2)
d = 2400√2/(60√2)
d = 40




Um abraço.

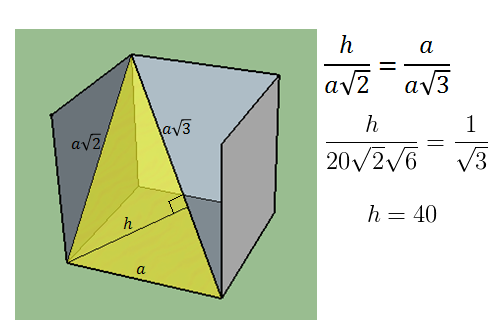
Um desenho da resolução do Ivomilton. 

São dois Pitágoras fáceis (que muita gente já tem prontos de cabeça). Depois também se pode usar semelhança de triângulos. A questão pode ser resolvida em 3 minutos.

Medeiros escreveu:Um desenho da resolução do Ivomilton. 

Muito obrigado, Medeiros, por seu auxílio colocando a ilustração que fala por si.
Como eu não consigo colocar desenhos, apelo sempre para a descrição...



Um abraço.