Números complexos

por marcoscastelobranco Qui 16 Out 2014, 04:45

resolva a equação
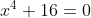
$Números complexos Gif$

como se faz pra achar as raízes dessa equação?

por PedroCunha Qui 16 Out 2014, 07:48

Olá, Marcos.

Aqui devemos aplicar a Segunda Lei de DeMoivre.

Veja:

x^4 + 16 = 0 \therefore x^4 = -16 \therefore x^4 = 16 \cdot -1 \rightarrow x^4 = 16 \cdot \operatorname{cis} \pi

Da Segunda Lei de DeMoivre, as raízes são tais que:

x = 2 \cdot \operatorname{cis} \left( \frac{\pi + 2k\pi}{4} \right), k = 0,1,2,3

Logo, são elas:

\\ \begin{cases} k = 0: x_1 = 2 \cdot \operatorname{cis} \left( \frac{\pi}{4} \right) \therefore x_1 = \sqrt{2} + i\sqrt{2} \\ k = 1: x_2 = 2 \cdot \operatorname{cis} \left( \frac{3\pi}{4} \right) \therefore x_2 = -\sqrt{2} + i\sqrt{2} \\ k=2: x_3 = 2 \cdot \operatorname{cis} \left( \frac{5\pi}{4} \right) \therefore x_3 = -\sqrt{2} - i\sqrt{2} \\ k=3: x_3 =2 \cdot \operatorname{cis} \left( \frac{7\pi}{4} \right) \therefore x_4 = \sqrt{2}-i\sqrt{2} \end{cases}

Sugiro estudar as duas Leis de DeMoivre.

Att.,
Pedro

por marcoscastelobranco Qui 16 Out 2014, 15:20

Obrigado , Pedro, vou dar uma olhada, abraço! Smile

por Conteúdo patrocinado

Números complexos

Números complexos

Re: Números complexos

Re: Números complexos

Re: Números complexos

Um fórum livre e democrático.