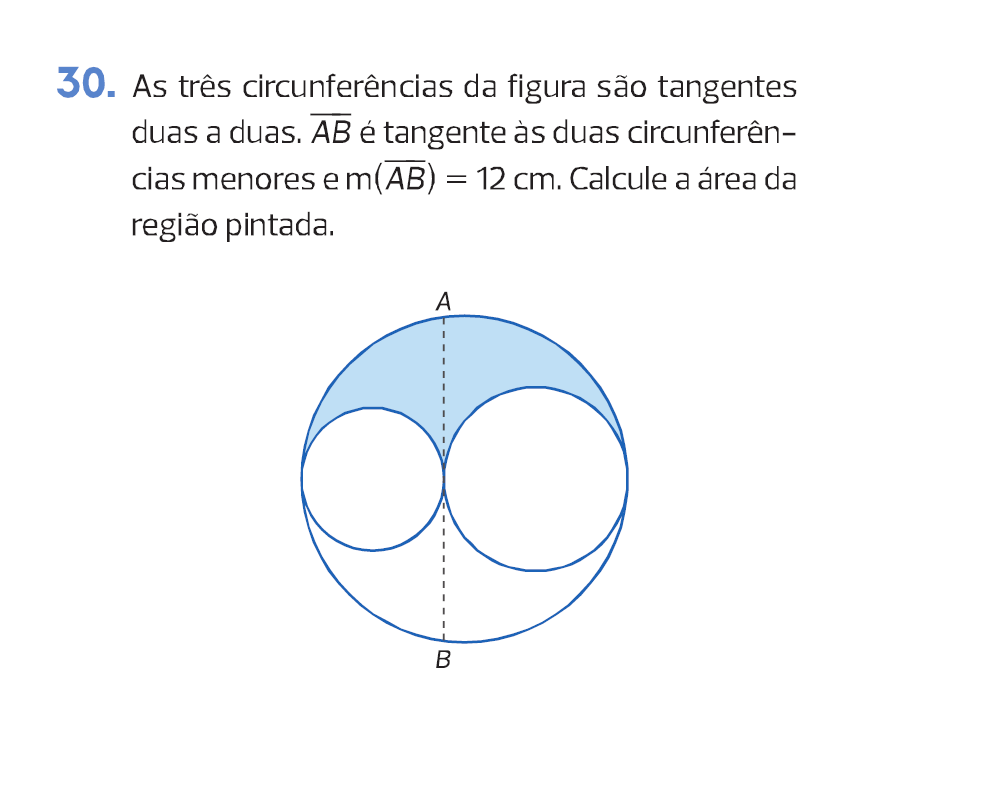
área hachurada

por rodocarnot Sáb 09 Ago 2014, 13:54

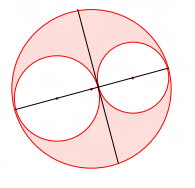
Dois círculos se tangenciam externamente e tangenciam internamente a um terceiro círculo (veja a ilustração). Se os centros dos três círculos são colineares, e a corda do terceiro círculo que é tangente aos outros dois em seu ponto de tangência, mede 20, qual a área da região interna ao terceiro círculo e externa aos outros dois?

área hachurada Oqg40m

Gabarito : 50 ∏

por **ivomilton** Sáb 09 Ago 2014, 16:16

rodocarnot escreveu:Dois círculos se tangenciam externamente e tangenciam internamente a um terceiro círculo (veja a ilustração). Se os centros dos três círculos são colineares, e a corda do terceiro círculo que é tangente aos outros dois em seu ponto de tangência, mede 20, qual a área da região interna ao terceiro círculo e externa aos outros dois?

Gabarito : 50 ∏

Boa tarde,

Essa questão tem muito a ver com esta outra:

https://pir2.forumeiros.com/t15476-circulos-tangentes

Um abraço.

por **raimundo pereira** Sáb 09 Ago 2014, 16:35

Sim tem tudo haver. Siga o desenho do mestre Euclides e vai encontrar 2R.2r=10.10---->R.r=25

O raio do círculo maior R=(2R+_2r)/2=R+r

ärea pedida = metade da área do círculo de raio (R+r) - metade da soma das áreas dos c'rculos de R e raio r.

por **ivomilton** Sáb 09 Ago 2014, 16:49

raimundo pereira escreveu:Sim tem tudo haver. Siga o desenho do mestre Euclides e vai encontrar 2R.2r=10.10---->R.r=25

O raio do círculo maior R=(2R+_2r)/2=R+r

ärea pedida = metade da área do círculo de raio (R+r) - metade da soma das áreas dos c'rculos de R e raio r.

Boa tarde, Raimundo.

Estou chegando lá agora; só que estou considerando que a área pedida é igual a:
Área do círculo de raio (R+r) - soma das áreas dos círculos de raios R e r, a saber:
∏(R+r)² - (∏R² + ∏r²) = ∏(R² + 2Rr + r² - R² - r²) = ∏(2Rr)

Como Rr=25, fica:
∏(2Rr) = ∏(2*25) = 50∏

Um abraço.

por **raimundo pereira** Sáb 09 Ago 2014, 16:51

Boa Tarde Ivomilton - é isso ai.

por rodocarnot Sáb 09 Ago 2014, 18:42

ivomilton escreveu:
raimundo pereira escreveu:Sim tem tudo haver. Siga o desenho do mestre Euclides e vai encontrar 2R.2r=10.10---->R.r=25

O raio do círculo maior R=(2R+_2r)/2=R+r

ärea pedida = metade da área do círculo de raio (R+r) - metade da soma das áreas dos c'rculos de R e raio r.
Boa tarde, Raimundo.

Estou chegando lá agora; só que estou considerando que a área pedida é igual a:
Área do círculo de raio (R+r) - soma das áreas dos círculos de raios R e r, a saber:
∏(R+r)² - (∏R² + ∏r²) = ∏(R² + 2Rr + r² - R² - r²) = ∏(2Rr)

Como Rr=25, fica:
∏(2Rr) = ∏(2*25) = 50∏

Um abraço.

Mestre , segui os passos do elcio , porém não consegui resolver o sistema final . Mas agora ta simplificado !!