área hachurada
3 participantes
Página 1 de 1
área hachurada
por rodrigomr Seg 06 Ago 2012, 17:27
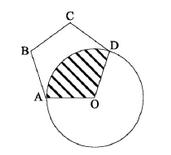
A figura mostra uma circunferência de centro O e raio igual a 2 e um pentágono regular ABCDO, cujos vértices A e D pertencem à circunferência. A região hachurada tem área igual a:
gabarito: 6∏/5
gabarito: 6∏/5
rodrigomr- Mestre Jedi
- Mensagens : 647
Data de inscrição : 13/04/2011
Idade : 32
Localização : Lavras, Minas Gerais, Brasil
Re: área hachurada
por parofi Seg 06 Ago 2012, 17:56
Olá:
Podemos determinar a medida de um ângulo interno do pentágono regular.
Como a soma dos ângulos de um polígono de n lados é (n-2).180º, então a soma dos ângulos de um pentágono é igual a (5-2).180º=540º. Como é um pentágono regular, cada ângulo interno mede 540º/5=108º.
Ora, a área de um setor circular é diretamente proporcional âo ângulo ao cento.
Logo, pi.2^2---360º
x---------108º, donde vem x=108x4 pi/360º = 6pi/5.
Podemos determinar a medida de um ângulo interno do pentágono regular.
Como a soma dos ângulos de um polígono de n lados é (n-2).180º, então a soma dos ângulos de um pentágono é igual a (5-2).180º=540º. Como é um pentágono regular, cada ângulo interno mede 540º/5=108º.
Ora, a área de um setor circular é diretamente proporcional âo ângulo ao cento.
Logo, pi.2^2---360º
x---------108º, donde vem x=108x4 pi/360º = 6pi/5.
parofi- Grupo
Velhos amigos do Fórum
- Mensagens : 495
Data de inscrição : 28/01/2012
Idade : 64
Localização : Vila Real-PORTUGAL
Re: área hachurada
por raimundo pereira Seg 06 Ago 2012, 18:06
Rodrigo,
Âng interno do pentágono ai5 ={(n-2).180}/n = 108º
Transformando em radianos.
180>>pi
108>>x >> x=(108/180). pi >>> x=(3/5)pi
S setor = {(3/5)pi . r²}/2 = (3/5)pi.4= 12pi/2.5 =6pi/5
Raimundo
Âng interno do pentágono ai5 ={(n-2).180}/n = 108º
Transformando em radianos.
180>>pi
108>>x >> x=(108/180). pi >>> x=(3/5)pi
S setor = {(3/5)pi . r²}/2 = (3/5)pi.4= 12pi/2.5 =6pi/5
Raimundo
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
