descobriR a reta tangente ao gráfico
5 participantes
Página 1 de 1
 descobriR a reta tangente ao gráfico
descobriR a reta tangente ao gráfico
seja r uma reta que passa por (1, -1) e é tangente ao gráfico de f(x)= x³-x. determine r.
leopinna- Mestre Jedi

- Mensagens : 939
Data de inscrição : 07/05/2013
Idade : 29
Localização : Rio de Janeiro - RJ
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Minha opnião é que algo no enunciado está errado pois a reta é secante no gráfico f(x)=x³-x, eu só acho..
ou nem entender a pergunta eu entendi =x
ou nem entender a pergunta eu entendi =x

jarry15- Recebeu o sabre de luz

- Mensagens : 115
Data de inscrição : 17/04/2014
Idade : 30
Localização : Boa Vista, RR, BR
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Também acho mas obrigado mesmo assim.
leopinna- Mestre Jedi

- Mensagens : 939
Data de inscrição : 07/05/2013
Idade : 29
Localização : Rio de Janeiro - RJ
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Olá 
Tentei usando cálculo.
Aplicando o conceito de reta tangente ao gráfico de=x^3-x) no ponto de intercessão
no ponto de intercessão ) :
:

então como a reta tangente passa por) , temos:
, temos:
\cdot(x-1))
aplicado o ponto) na equação da reta :
na equação da reta :
\cdot(x_{0}-1))
fazendo a intercessão com a função aplicada no ponto de intercessão : , obtemos :
, obtemos :
&space;\;\;\;&space;\wedge&space;\;\;\;&space;(\frac{3}{2}&space;\;&space;,&space;\;&space;\frac{15}{8}&space;))
Aplicando este pontos na equação da reta tangente temos que somente o primeiro satisfaz.
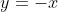
e ainda há uma reta vertical :
Tentei usando cálculo.
Aplicando o conceito de reta tangente ao gráfico de
então como a reta tangente passa por
aplicado o ponto
fazendo a intercessão com a função aplicada no ponto de intercessão :
Aplicando este pontos na equação da reta tangente temos que somente o primeiro satisfaz.
e ainda há uma reta vertical :
Última edição por Man Utd em Qua 11 Jun 2014, 22:42, editado 1 vez(es)

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Man Utd
Tenho apenas uma dúvida: as raízes da função são x = -1, x = 0, x = 1
Plotei o gráfico de y = x³ - x no Wolfram e, com o mouse marquei o ponto (1, -1)
Dá para ver que a origem (0, 0) pode ser um ponto de tangência.
Mas, também dá para ver que existe outro ponto de tangência no 1º quadrante.
Neste caso existiriam DUAS retas que atendem, E a solução algébrica não mostra esta outra reta!
Como explicar?
Tenho apenas uma dúvida: as raízes da função são x = -1, x = 0, x = 1
Plotei o gráfico de y = x³ - x no Wolfram e, com o mouse marquei o ponto (1, -1)
Dá para ver que a origem (0, 0) pode ser um ponto de tangência.
Mas, também dá para ver que existe outro ponto de tangência no 1º quadrante.
Neste caso existiriam DUAS retas que atendem, E a solução algébrica não mostra esta outra reta!
Como explicar?

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Elcioschin escreveu:Man Utd
Tenho apenas uma dúvida: as raízes da função são x = -1, x = 0, x = 1
Plotei o gráfico de y = x³ - x no Wolfram e, com o mouse marquei o ponto (1, -1)
Dá para ver que a origem (0, 0) pode ser um ponto de tangência.
Mas, também dá para ver que existe outro ponto de tangência no 1º quadrante.
Neste caso existiriam DUAS retas que atendem, E a solução algébrica não mostra esta outra reta!
Como explicar?
Bem se a outra reta for vertical, não há como achar usando derivadas já que nem existiria a derivada e tbm não poderia usar a fórmula de reta tangente

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
A outra reta não é vertical
Poste a função no Wolfram e veja você mesmo
Poste a função no Wolfram e veja você mesmo

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Só há uma tangente (aquela calculada por derivação). O ponto (0,0) é um ponto de inflexão da curva e não há tangente nesse ponto.


____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: descobriR a reta tangente ao gráfico
Re: descobriR a reta tangente ao gráfico
Euclides escreveu:Só há uma tangente (aquela calculada por derivação). O ponto (0,0) é um ponto de inflexão da curva e não há tangente nesse ponto.
Bom dia
Euclides, não entendi o pq de não existir reta tangente no ponto de inflexão.Já que uma das condições para ser ponto de inflexão é que exista reta tangente.
A reta que vc esboçou é secante, veja o gráfico "mais de longe" :

Aguardo a opinião de todos.
Muito Obrigado pela atenção.

Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 30
Localização : Manchester
 Tópicos semelhantes
Tópicos semelhantes» Descobrir equação da reta
» Descobrir a equação da reta
» 24: reta tangente ao gráfico
» Como descobrir a função a partir do gráfico?
» Descobrir a equação da reta
» Descobrir a equação da reta
» 24: reta tangente ao gráfico
» Como descobrir a função a partir do gráfico?
» Descobrir a equação da reta
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












