OBM 2007
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
OBM 2007
por iaguete Ter 14 Jan 2014, 23:20
O conjunto dos valores de c para os quais a equação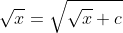 
possui solução real está contido em:
a)[-1,օօ[
b)]-օօ,1]
c)[-3,2]
d)[-2,3]
e)Z
gabarito: a
Eu tentei fazer da seguinte forma.
x=√x+c
x-c=√x
x²-2xc+c²=x
x²-2xc-x+c²=0
x²-x(2c+1)+c²=0
∆=(2c+1)²-4.c²=4c²+4c+1-4c²>=0
4c>=-1
c>=-1/4
e não tem opção que bata.
a)[-1,օօ[
b)]-օօ,1]
c)[-3,2]
d)[-2,3]
e)Z
gabarito: a
Eu tentei fazer da seguinte forma.
x=√x+c
x-c=√x
x²-2xc+c²=x
x²-2xc-x+c²=0
x²-x(2c+1)+c²=0
∆=(2c+1)²-4.c²=4c²+4c+1-4c²>=0
4c>=-1
c>=-1/4
e não tem opção que bata.
iaguete- Jedi
- Mensagens : 253
Data de inscrição : 13/05/2012
Idade : 30
Localização : rio de janeiro
Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
Re: OBM 2007
por iaguete Ter 14 Jan 2014, 23:53
Ah sim hahaha. eu resolvi a questão e nem me toquei :/ ... é porque sempre me enrolo com essa parada de sinal, sempre caio no erro de ler pelo valor numerico e esquecer o sinal.Luck escreveu:Tem opção sim, leia novamente o enunciado!
iaguete- Jedi
- Mensagens : 253
Data de inscrição : 13/05/2012
Idade : 30
Localização : rio de janeiro
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
