polinomios
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
polinomios
por martinfierro76 Qui 19 Dez 2013, 15:15
Sejam z e w as duas raizes não reais do polinomio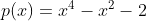 
. Nestas condições é INCORRETO afirmar que
A. (z-w) é um numero imaginario puro.
B. z=-w
C.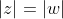
D. (zw) é um numero real positivo.
E. (z+w) é um numero real irracional.
como diz o exercicio que tiene duas raices não reais, tentei achar as raices reais con ruffini, e tntão de aí achar a raices irracionales desde el polinomio de sendo grado. Mais testando +1.-1.2.-2, não achei raices em nungum deses numeros
A. (z-w) é um numero imaginario puro.
B. z=-w
C.
D. (zw) é um numero real positivo.
E. (z+w) é um numero real irracional.
como diz o exercicio que tiene duas raices não reais, tentei achar as raices reais con ruffini, e tntão de aí achar a raices irracionales desde el polinomio de sendo grado. Mais testando +1.-1.2.-2, não achei raices em nungum deses numeros
martinfierro76- Jedi
- Mensagens : 265
Data de inscrição : 11/02/2013
Idade : 48
Localização : foz do iguaçu
Re: polinomios
por PedroCunha Qui 19 Dez 2013, 15:43
Fazendo x² = y:
y² - y - 2 = 0
y' = (1 + 3)/2 --> y' = 2
y'' = (1-3)/2 --> y' = -1
Voltando:
x² = y'
x² = 2 --> x = ±√2
x² = y''
x² = -1 --> x = ±i
Partindo para as alternativas:
A: z -w = i - (-i) = 2i --> Imaginário Puro
B: z = -w --> z = i, w = -i --> z = -w
C: |z| = |w| --> |z| = √(0² + 1²) = √1 = 1 , |w| = √(0² + (-1)²) = √1 =1 --> |z| = |w|
D: zw = i * (-i) = -i² = -(-1) = 1 --> Real Positivo
E: z + w = i + (-i) = 0 --> Número natural --> Afirmativa incorreta
Att.,
Pedro
y² - y - 2 = 0
y' = (1 + 3)/2 --> y' = 2
y'' = (1-3)/2 --> y' = -1
Voltando:
x² = y'
x² = 2 --> x = ±√2
x² = y''
x² = -1 --> x = ±i
Partindo para as alternativas:
A: z -w = i - (-i) = 2i --> Imaginário Puro
B: z = -w --> z = i, w = -i --> z = -w
C: |z| = |w| --> |z| = √(0² + 1²) = √1 = 1 , |w| = √(0² + (-1)²) = √1 =1 --> |z| = |w|
D: zw = i * (-i) = -i² = -(-1) = 1 --> Real Positivo
E: z + w = i + (-i) = 0 --> Número natural --> Afirmativa incorreta
Att.,
Pedro
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
Re: polinomios
por martinfierro76 Qui 19 Dez 2013, 17:25
obrigado, só fiquei com uma duvida, o que fez na alternativa C?, o qeu são os numeros 0 , 1 e -1?
martinfierro76- Jedi
- Mensagens : 265
Data de inscrição : 11/02/2013
Idade : 48
Localização : foz do iguaçu
Re: polinomios
por Elcioschin Qui 19 Dez 2013, 17:59
z = i ----> z = 0 + 1.i ----> |z|² = 0² + 1² ----> |z|² = 1 ---> |z| = 1
w = -i ---> w = 0 - 1.i ---> |w|² = 0² + (-1)² ---> |w|² = 1 ---> |w| = 1
w = -i ---> w = 0 - 1.i ---> |w|² = 0² + (-1)² ---> |w|² = 1 ---> |w| = 1
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: polinomios
por PedroCunha Qui 19 Dez 2013, 18:00
Veja:
Dado um número complexo qualquer Z, tal que Z = a + bi, seu módulo é representado por:
|Z| = ρ (rô) = √(a²+b²)
No caso do exercício:
z = i ou seja z = 0 +1i
Logo: |z| = √(0² + 1²) = √1 = 1
w = -i ou seja w = 0 - 1i
Logo: |z| = √(0² + (-1)²) = √1 = 1
Entendeu?
Att.,
Pedro
Dado um número complexo qualquer Z, tal que Z = a + bi, seu módulo é representado por:
|Z| = ρ (rô) = √(a²+b²)
No caso do exercício:
z = i ou seja z = 0 +1i
Logo: |z| = √(0² + 1²) = √1 = 1
w = -i ou seja w = 0 - 1i
Logo: |z| = √(0² + (-1)²) = √1 = 1
Entendeu?
Att.,
Pedro
PedroCunha- Monitor
- Mensagens : 4639
Data de inscrição : 13/05/2013
Idade : 28
Localização : Viçosa, MG, Brasil
martinfierro76- Jedi
- Mensagens : 265
Data de inscrição : 11/02/2013
Idade : 48
Localização : foz do iguaçu
Tópicos semelhantesPiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
