Somatórios e Produtórios
2 participantes
Página 1 de 1
 Somatórios e Produtórios
Somatórios e Produtórios
Se 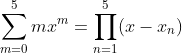 , calcule
, calcule 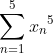 .
.

Dela Corte- Recebeu o sabre de luz

- Mensagens : 197
Data de inscrição : 31/05/2013
Idade : 27
Localização : Jacareí, São Paulo
 Re: Somatórios e Produtórios
Re: Somatórios e Produtórios
x + 2x² + 3x³ + 4x^4 + 5x^5 = (x-x1)(x-x2)(x-x3)(x-x4)(x-x5)
Note que x1,x2,x3,x4,x5 são as raízes do polinômio 5x^5 + 4x^4 + 3x³ + 2x² + x
sendo uma das raízes zero, se reduz a 5x^4 + 4x³ + 3x² +2x + 1
x1^5 + x2^5 + x3^5 + x4^5 , S[5] = ?
Usando somas de newton, temos:
5S[n] = -4S[n-1] -3S[n-2] -2S[n-3] - 1S[n-4]
5S[3] = -4S[2] - 3S[1] - 2S[0] - S[-1]
S[-1] = x1^(-1)+ x2^(-1) + x3^(-1) + x4^(-1) = [x2x3x4 + x1x3x4 + x1x2x4 + x1x2x2 + x1x2x3x4] / (x1x2x3x4)
que por girard: S[-1] = (-2/5)/(1/5) = -2
S[0] = 5 ; S[1] = (-4/5)
S[2] = S[1]² - 2(3/5) = 4 - (6/5) = 14/5
S[3] = -4(14/5) - 3(-4/5) -2(-2) + (-1).5
S[3] = -49/5
S[4] = -4(-49/5) - 3(14/5) -2(-4/5) + (-1)(-2)
S[4] = 172/5
S[5] = -4(172/5) -3(-49/5) -2(14/5) + (-1)(-4/5)
S[5] = -113
favor, verifique as contas..
Note que x1,x2,x3,x4,x5 são as raízes do polinômio 5x^5 + 4x^4 + 3x³ + 2x² + x
sendo uma das raízes zero, se reduz a 5x^4 + 4x³ + 3x² +2x + 1
x1^5 + x2^5 + x3^5 + x4^5 , S[5] = ?
Usando somas de newton, temos:
5S[n] = -4S[n-1] -3S[n-2] -2S[n-3] - 1S[n-4]
5S[3] = -4S[2] - 3S[1] - 2S[0] - S[-1]
S[-1] = x1^(-1)+ x2^(-1) + x3^(-1) + x4^(-1) = [x2x3x4 + x1x3x4 + x1x2x4 + x1x2x2 + x1x2x3x4] / (x1x2x3x4)
que por girard: S[-1] = (-2/5)/(1/5) = -2
S[0] = 5 ; S[1] = (-4/5)
S[2] = S[1]² - 2(3/5) = 4 - (6/5) = 14/5
S[3] = -4(14/5) - 3(-4/5) -2(-2) + (-1).5
S[3] = -49/5
S[4] = -4(-49/5) - 3(14/5) -2(-4/5) + (-1)(-2)
S[4] = 172/5
S[5] = -4(172/5) -3(-49/5) -2(14/5) + (-1)(-4/5)
S[5] = -113
favor, verifique as contas..

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: Somatórios e Produtórios
Re: Somatórios e Produtórios
Olá Luck,
Não entendi o porquê de duas coisas:
- excluir a raíz = 0 do Girard e das Somas de Newton
- calcular S[-1] e S[0]
Grato.
Não entendi o porquê de duas coisas:
- excluir a raíz = 0 do Girard e das Somas de Newton
- calcular S[-1] e S[0]
Grato.

Dela Corte- Recebeu o sabre de luz

- Mensagens : 197
Data de inscrição : 31/05/2013
Idade : 27
Localização : Jacareí, São Paulo
 Re: Somatórios e Produtórios
Re: Somatórios e Produtórios
A equação é p(x) = x(5x^4 + 4x³ + 3x² +2x + 1) como sabemos que x = 0 é raíz (x5^5 = 0), logo as outras quatro raízes são diferentes de 0 , note então que agora estamos analisando uma equação de quarto grau nas somas de Newton, q(x) = 5x^4 + 4x³ + 3x² + 2x + 1, então basta cacular o S[5] de q(x) , e para isso é necessário ter o valor de S[-1] para obter S[3], ja que n seria possível calcular S[4] sem antes ter o valor de S[3] , e assim S[5]...Dela Corte escreveu:Olá Luck,
Não entendi o porquê de duas coisas:
- excluir a raíz = 0 do Girard e das Somas de Newton
- calcular S[-1] e S[0]
Grato.

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: Somatórios e Produtórios
Re: Somatórios e Produtórios
Muitíssimo obrigado.

Dela Corte- Recebeu o sabre de luz

- Mensagens : 197
Data de inscrição : 31/05/2013
Idade : 27
Localização : Jacareí, São Paulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












