Interseção Hipérbole e Circunferência

por Berchades Sáb 08 Jun 2013, 11:13

Considere o círculo 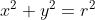$x^2+y^2=r^2$ de raio r e a hipérbole $x^2-y^2=1$ . Nesse caso, pode-se afirmar que:

a) se r < 1, então as curvas se intersectam em quatro pontos.
b) se r = 1, então as curvas têm quatro pontos em comum.
c) se r =1, as curvas se intersectam em (0,1) e (0,-1)
d) se r= V17, então as curvas se intersectam apenas nos pontos (3,2V2) e (3,-2V2).
e) se r > V17, então as curvas se intersectam em quatro pontos.

R: e)

por **Elcioschin** Sáb 08 Jun 2013, 14:26

Faça um desenho num sistema xOY da hipérbole ----> a = 1, b = 1 ----> V(-1, 0) e V'(1, 0)

a) Se r < 1 ----> Não existe interseção ----> Errado
b) Se r = 1----> Existem 2 pontos de interseção: os vértices V e V' ----> Errado
c) Se r = 1 ----> V(-1, 0) e V'(1, 0) ----> ERrado
d)
x² + y² = r² ---->I
x² - y² = 1 ----> x² = y² + 1 ----> II

Ii em I ---> (y² + 1) + y² = r² ----> 2y² = r² - 1 ----> y² = (r² - 1)/2

I ---> x² + (r² - 1)/2 = r² ----> x² = r² + (r² - 1)/2 ---> x² = (r² + 1)/2

Para r = \/17 ----> x² = (17 + 1)/2 ----> x² = 9 ----> x = ± 3 ----> y² = (17 - 1)/2 ----> y = ± 2

Pontos de interseção ----> (- 3, 2), (-3, -2), (3, 2), (3, -2) ----> Errado

E correto

Interseção Hipérbole e Circunferência

Interseção Hipérbole e Circunferência

Re: Interseção Hipérbole e Circunferência

Um fórum livre e democrático.