Máximos e Mínimos
2 participantes
Página 1 de 1
Máximos e Mínimos
por Giiovanna Qui 30 maio 2013, 15:10
É possívelfazer um retângulo com área máxima inscrito na elipse de equação (x^2)/16 + (y^2)/9 = 1 e que tenha seus lados paralelos aos eixos coordenados?
Justifique e, caso seja possível, calcule a medida de seus lados.
Vou colocar o que fiz até agora:
Seja P(x,y) um ponto sobre essa elipse. Como esse triângulo tem lados paralelos aos eixos coordenados, temos que sua área pode ser escrita como:
A = 2x . 2y = 4.x.y
Como P está sobre a elipse, podemos escrever que:
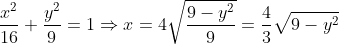
E, então:
&space;=&space;\frac{16}{3}y\sqrt{9-y^2})
(pode ser que eu tenha errado alguma conta).
Bastaria verificar se essa função tem ponto de máximo global? Ou não necessariamente?
Obrigada.
Justifique e, caso seja possível, calcule a medida de seus lados.
Vou colocar o que fiz até agora:
Seja P(x,y) um ponto sobre essa elipse. Como esse triângulo tem lados paralelos aos eixos coordenados, temos que sua área pode ser escrita como:
A = 2x . 2y = 4.x.y
Como P está sobre a elipse, podemos escrever que:
E, então:
Bastaria verificar se essa função tem ponto de máximo global? Ou não necessariamente?
Obrigada.
Giiovanna- Grupo
Velhos amigos do Fórum
- Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Máximos e Mínimos
por Euclides Qui 30 maio 2013, 16:03
Legal Giiovanna, é isso. Você encontrou a função que descreve a área do retângulo procurado. Se ela tiver um máximo (único) então será possível o retângulo de área máxima.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Re: Máximos e Mínimos
por Giiovanna Qui 30 maio 2013, 16:13
Oi Euclides.
Fiz diferente, usei em função de x pois ficou mais fácil para derivar. Mas enfim, achei esse máximo único que seria no ponto x = V8 = 2V2.
Notei que a função A (que eu fiz, agora, em função de x) é definida apenas -4 <= x <= 4 (e ela é contínua). Então, pelo Teorema de Weierstrass, a função assume máximo e mínimo. Seria de se esperar, então, que conseguissemos achar um x e um y tal que a área desse retângulo seja máxima, certo?
Fiz diferente, usei em função de x pois ficou mais fácil para derivar. Mas enfim, achei esse máximo único que seria no ponto x = V8 = 2V2.
Notei que a função A (que eu fiz, agora, em função de x) é definida apenas -4 <= x <= 4 (e ela é contínua). Então, pelo Teorema de Weierstrass, a função assume máximo e mínimo. Seria de se esperar, então, que conseguissemos achar um x e um y tal que a área desse retângulo seja máxima, certo?
Giiovanna- Grupo
Velhos amigos do Fórum - Mensagens : 2128
Data de inscrição : 31/08/2012
Idade : 30
Localização : São Paulo, SP
Re: Máximos e Mínimos
por Euclides Qui 30 maio 2013, 16:21
Isso.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
