Máximo e Mínimo

Como calcular máximos e mínimos de uma função ? E como determinar se tal é crescente ou decrescente ? Obrigado

O máximo e mínimo da função são calculados através da derivada primeira de uma função. Quando essa derivada primeira dá zero, os valores para os quais isso acontecem podem ser ponto de máximo, ponto de mínimo ou ponto onde a função de inflexão. Para saber qual dos três é, se faz o teste da derivada segunda. Caso a derivada segunda para esse valor seja positiva, é ponto de mínimo; caso a derivada segunda seja negativa, é ponto de máximo e caso seja zero, é ponto de inflexão.

E, para saber se a função crescente ou decrescente basta ver onde a derivada primeira dá zero e estudar os sinais dessa derivada primeira. Onde a derivada primeira for positiva, é onde a função é crescente e onde a derivada primeira for negativa, é onde a função é decrescente. Derivada primeira igual a zero indica troca de crescente para decrescente.

Espero ter ajudado. ^_^

Esteves, muito boa sua explicação, mas teria como fazer um exemplo pra ver se eu entendi corretamente ? Obrigado

Claro. Por exemplo, nós sabemos como é a função f(x) = x² - 5x + 6.
Para começar, vamos tirar a derivada primeira e a derivada segunda:
f'(x) = 2x - 5
f''(x) = 2
Como pode ver, a derivada segunda é uma constante positiva. Então a concavidade de f(x) é sempre para cima. Isso pode ser confirmado, pois temos um conhecimento prévio da função.
Agora, quando a derivada primeira der zero, o ponto para o qual isso acontecer vai ser ponto de mínimo, pois como f''(x) > 0, não tem como termos valores de máximo e nem pontos de inflexão, já que a concavidade nem muda.
Então...
f'(x) = 2x - 5 = 0 -> 2x = 5 -> x = 5/2
Então, de acordo com isso, temos que em x = 5/2 temos o valor mínimo dessa função. Como temos um conhecimento prévio desse tipo de função, já podemos inclusive fazer dos meios que já sabemos que dá certo para ver se esse método também é funcional.
Xvértice = - b / 2a = - (- 5) / 2 = 5/2
Então x = 5/2 é ponto de mínimo mesmo!

Repare que para valores menores que 5/2, f'(x) < 0; e para valores maiores que 5/2, f'(x) > 0. Isso significa que quando x < 5/2, a função é decrescente e quando x > 5/2, a função é crescente.

Consegui provar para você que com essa função do segundo grau deu certo e posso provar para qualquer função do segundo grau inclusive. Entretanto, não tenho como te provar para outras funções, mas tenho certeza que esse método funciona para várias outras, inclusive funções não-polinomiais.

Espero ter ajudado de novo. ^_^

O limite que expressa a inclinação da tangente ao ponto x₀ é a definição da derivada de f(x) no ponto

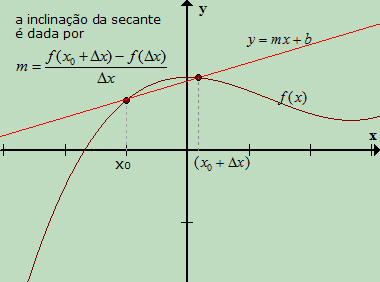
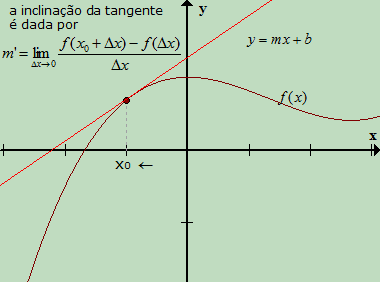
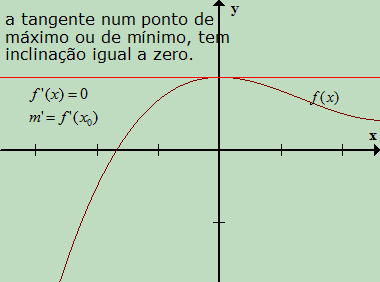
Obrigada pela ajuda, Euclides!
Tinha até me esquecido dessa demonstração gráfica.

Lembrando que pontos onde a inclinação é zero também podem ser pontos de inflexão como x = 0 na função f(x) = x³. Nesse caso, f''(x) = 0 também.

Obrigado a todos, muito boa as explicações !