CN 1981 - área de figura geométrica
4 participantes
Página 1 de 1
CN 1981 - área de figura geométrica
por raimundo pereira Sex Ago 10 2012, 18:06
Uma figura de 6 pontas é obtida pela arrumação de dois triângulos equiláteros circunscritos ao círculo de 4cm de raio, de maneira que os lados fiquem 2 a 2 paralelos. Qual é a área dessa figura?
a)32V3cm²
b)64V3cm²
c)96V3cm²
d)36V3cm²
e)72V3cm²
Gabarito letra B
a)32V3cm²
b)64V3cm²
c)96V3cm²
d)36V3cm²
e)72V3cm²
Gabarito letra B
raimundo pereira- Grupo
Velhos amigos do Fórum
- Mensagens : 6113
Data de inscrição : 13/06/2012
Idade : 82
Localização : Rio de Janeiro
Re: CN 1981 - área de figura geométrica
por Al.Henrique Sex Ago 10 2012, 19:01
Amigos,
Me parece que ele quer a área dos dois triângulos...
Não achei gabarito.
Me parece que ele quer a área dos dois triângulos...
Não achei gabarito.
Al.Henrique- Grupo
Velhos amigos do Fórum - Mensagens : 1203
Data de inscrição : 13/03/2012
Idade : 33
Localização : Rio de Janeiro -
Re: CN 1981 - área de figura geométrica
por raimundo pereira Sex Ago 10 2012, 19:40
Olá Al Henrique,
Creio que não seja esta a figura . Na minha concepção o círculo está inscrito nos triângulos equiláteros. Acho que a solução vem por uma subtração de áreas. att
Raimundo
Creio que não seja esta a figura . Na minha concepção o círculo está inscrito nos triângulos equiláteros. Acho que a solução vem por uma subtração de áreas. att
Raimundo
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6113
Data de inscrição : 13/06/2012
Idade : 82
Localização : Rio de Janeiro
Re: CN 1981 - área de figura geométrica
por raimundo pereira Sex Ago 10 2012, 20:05
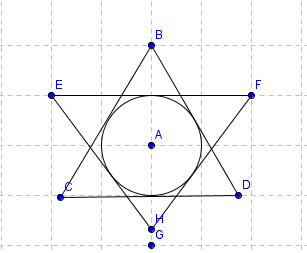
Será esta a imagem?
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6113
Data de inscrição : 13/06/2012
Idade : 82
Localização : Rio de Janeiro
Não resolvido
por raimundo pereira Sáb Ago 11 2012, 09:02
Gostaria de ouvir opiniões sobre a figura correta para o enunciado desse problema att
Raimundo
Raimundo
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6113
Data de inscrição : 13/06/2012
Idade : 82
Localização : Rio de Janeiro
Re: CN 1981 - área de figura geométrica
por Elcioschin Sáb Ago 11 2012, 11:53
O desenho do Raimundo está correto
Sejam M, N, P, Q, S. T os pontos de tanência no sentido horário sendo M o ponto superior
Seja L o lado de cada triângulo e R o raio do círculo:
GÊF = 60º ----> MÂS = 120º
Trace MS
EM*cos30º + R*cos60º + R = R*cos30º ---> (L/2)*\/3/2 + R/2 + R = L*\/3/2 ---> L*\/3/4 = 3R/2 ----> L = 2*\/3*R
S = 12*[(2*R*\/3)/3]²*\/3/4 -----> S = 4*\/3*R² ----> S = 4*\/3*4² ----> S = 64*\/3
Sejam M, N, P, Q, S. T os pontos de tanência no sentido horário sendo M o ponto superior
Seja L o lado de cada triângulo e R o raio do círculo:
GÊF = 60º ----> MÂS = 120º
Trace MS
EM*cos30º + R*cos60º + R = R*cos30º ---> (L/2)*\/3/2 + R/2 + R = L*\/3/2 ---> L*\/3/4 = 3R/2 ----> L = 2*\/3*R
S = 12*[(2*R*\/3)/3]²*\/3/4 -----> S = 4*\/3*R² ----> S = 4*\/3*4² ----> S = 64*\/3
Elcioschin- Grande Mestre
- Mensagens : 71773
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
Re: CN 1981 - área de figura geométrica
por raimundo pereira Sáb Ago 11 2012, 12:31
Bom dia mestre Elcio.
Obrigado. att
Raimundo
Obrigado. att
Raimundo
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6113
Data de inscrição : 13/06/2012
Idade : 82
Localização : Rio de Janeiro
Re: CN 1981 - área de figura geométrica
por JEABM Ter Mar 20 2018, 23:33
Boa nt! Raimundo teria a imagem p postar novamente? Grato
JEABM- Mestre Jedi
- Mensagens : 771
Data de inscrição : 18/06/2013
Idade : 38
Localização : Taubaté - SP
Re: CN 1981 - área de figura geométrica
por JEABM Ter Mar 27 2018, 13:46
Boa nt! Raimundo teria a imagem p postar novamente? Grato
JEABM- Mestre Jedi
- Mensagens : 771
Data de inscrição : 18/06/2013
Idade : 38
Localização : Taubaté - SP
Re: CN 1981 - área de figura geométrica
por Elcioschin Ter Mar 27 2018, 18:38
Veja: https://pir2.forumeiros.com/t58427-cn-1980-areas#515518
Elcioschin- Grande Mestre
- Mensagens : 71773
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
Tópicos semelhantes» Área de figura geométrica
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
» Figura geométrica
» Volume de uma figura geométrica
» Figura geometrica - valor de x
» (F.C.M. STA. CASA - 1981) Área do Triângulo com a Área do círculo
» Figura geométrica
» Volume de uma figura geométrica
» Figura geometrica - valor de x
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
