Parábola FUVEST-SP
3 participantes
Página 1 de 1
Parábola FUVEST-SP
por Fernando_Vieira Qui 02 Ago 2012, 11:19
(FUVEST-SP) É dada a parábola de equação
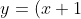.(x+a-1),\,a\in\mathbb{R})
.
Sejam r e s as retas tangentes à parábola nos pontos onde ela encontra o eixo dos x. DETERMINE a de modo que r seja perpendicular a s.
Fernando_Vieira- Padawan
- Mensagens : 56
Data de inscrição : 20/05/2012
Idade : 29
Localização : Belo Horizonte, MG Brasil
Re: Parábola FUVEST-SP
por parofi Qui 02 Ago 2012, 12:09
Olá:
Zeos da função y=f(x):
x+1=0 ٧ x+a-1=0, ou seja, x=-1 ٧ x=1-a.
F. Derivada: y'=1(x+a-1)+1(x+1)=2x+a.
Declive da tangente à curva, para x= -1: m=-2+a;
Declive da tangente à curva, para x=1-a: m'= 2(1-a)+a=2-a.
As tangentes são perpendiculares se -2+a = -1/(2-a), donde vem (-2+a)(2-a)=-1, ou seja (2-a)^2=1 ↔ 2-a =1 ou 2-a=-1, o que dá a=1 ou a=3.
Zeos da função y=f(x):
x+1=0 ٧ x+a-1=0, ou seja, x=-1 ٧ x=1-a.
F. Derivada: y'=1(x+a-1)+1(x+1)=2x+a.
Declive da tangente à curva, para x= -1: m=-2+a;
Declive da tangente à curva, para x=1-a: m'= 2(1-a)+a=2-a.
As tangentes são perpendiculares se -2+a = -1/(2-a), donde vem (-2+a)(2-a)=-1, ou seja (2-a)^2=1 ↔ 2-a =1 ou 2-a=-1, o que dá a=1 ou a=3.
parofi- Grupo
Velhos amigos do Fórum
- Mensagens : 495
Data de inscrição : 28/01/2012
Idade : 64
Localização : Vila Real-PORTUGAL
Re: Parábola FUVEST-SP
por Elcioschin Qui 02 Ago 2012, 12:15
Pontos onde a parábola encontra o eixo dos x ----> y = 0
x = -1 ----> y = 0 ----> P(-1, 0)
x = 1 - a ---> y = 0 ---> Q(1-a, 0)
Equação da parábola ----> y = (x + 1)*(x + a - 1) ----> y = x² + ax + (a - 1)
Equação das retas tagentes ----> y' = 2x + a
Ponto P(-1, 0) -----> y'P = 2*(-1) + a ----> y'P = a - 2
Ponto Q(1-a, 0) ----> y'Q = 2*(1-a) + a ----> y'Q = 2 - a
Para serm perpendiculares ----> (y'P)*(y'Q) = -1 ----> (a - 2)*(2 - a) = -1 ----> a² - 4a + 3 = 0 ---->
Raízes ---> a = 1 ou a = 3
x = -1 ----> y = 0 ----> P(-1, 0)
x = 1 - a ---> y = 0 ---> Q(1-a, 0)
Equação da parábola ----> y = (x + 1)*(x + a - 1) ----> y = x² + ax + (a - 1)
Equação das retas tagentes ----> y' = 2x + a
Ponto P(-1, 0) -----> y'P = 2*(-1) + a ----> y'P = a - 2
Ponto Q(1-a, 0) ----> y'Q = 2*(1-a) + a ----> y'Q = 2 - a
Para serm perpendiculares ----> (y'P)*(y'Q) = -1 ----> (a - 2)*(2 - a) = -1 ----> a² - 4a + 3 = 0 ---->
Raízes ---> a = 1 ou a = 3
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Tópicos semelhantesPágina 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
