Período de uma função.

Determine o período e a imagem e faça o gráfico de um período completo da função f: R -> R dada por f(x) = | cosx| .

Eu sei como fazer o gráfico da função, só não consigo indentificar por que o período vai ser pi. Alguém pode por favor me explicar como encontrar o período de uma função só de olhar para o gráfico? Eu sei que existe uma fórmula para calcular, mas eu quero entender pelo gráfico. Grato desde já !

Fala Pete!

Bom, se você sabe fazer o gráfico , certamente sabe fazer todo o resto!

Não é dificil de se enxergar que quando apenas colocamos um módulo em uma função, esta não tem imagem negativa.

Imagine a função cosx. O periodo da mesma é 2∏. Porém, ao se colocar o módulo nela, seu periodo reduz a ∏. Isso ocorre porque ela volta aos valores iniciais mais rapido. Antes ela precisava de 2∏ para voltar ao ponto inicial. Mas porque ? Porque ela ainda tinha que passar pelos y negativos do gráfico. Com o módulo, a função não faz mais isso..

Quando não temos módulo :

O periodo da função sen(kx) é 2∏/k
O periodo da função cos(kx) é 2∏/k

O periodo da função tg(kx) e cotg(kx) = ∏/k

Se tiver o módulo, será o periodo da sem módulo divido por 2.

Olá petebest007,

A função tem período igual a .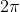

O período de uma função é um intervalo do domínio após o qual ela se repete. Vamos ver o gráfico dessa função:



A função é uma função modular e só possui valores positivos. Essa função é formada pelos valores positivos de cos(x) e pelo "rebatimento" dos valores negativos. Isso altera o período como se verá no gráfico a seguir:

Entendi !!!! Muito obrigado a vocês dois.