IME-1964

Prolonga-se o raio AO de um círculo,de um comprimento AB=AO;traça-se uma tangente ao círculo,sobre a qual se levantam as perpendiculares NA e BC.Supondo que o ângulo OÂC=126 graus,qual o valor do ângulo ACB?

Quem resolver a questão,gostaria de pedir para que fosse colocado o desenho.Agradeço desde já.

Você tem o gabarito ?

Legenda:

Traços cheios - Dados do enunciado.
Traços pontilhados - Prolongamentos que fiz.



Justificativas do desenho:

a)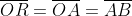

São segmentos iguais ao raio da circunferência (AB = Raio é do próprio enunciado).

b)

Basta ver que CNR é a projeção ortogonal de OAB sobre a reta tangente. Como na projeção ortogonal as proporções entre segmentos se mantém inalteradas, OA = AB implica proj(OA) = proj(AB) e claramente o triângulo com vértice em A é isósceles.

c)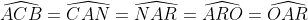

ACB e CAN são alternos internos; CAN e NAR são iguais pois AN é bissetriz; NAR e ARO são alternos internos;
ARO e OAR são ângulos opostos aos lados iguais do triângulo isósceles OAR.

Finalmente, segue:



Desculpem se algo não ficou claro. Tenho muita dificuldade em geometria plana...

Fiquei com uma dúvida.

Aproveitando o desenho do Robson.
Supondo-se que a reta tangente seja paralela ao raio OA do círculo. (Colocando o desenho no esquadro)

O ângulo OÂC = 126º , o seu suplemento é 180º-126º= 54º .

Veja agora o triângulo ACB (retangulo em B) , o ângulo A^CB= 180º-90º-54º= 36º

Onde errei? att Raimundo

Raimundo, na situação particular que você descreveu OAC não poderia ser 126º.

OAN valeria 90º.

NAC seria o ângulo entre um lado e a diagonal do quadrado, ou seja 45º.

Teríamos OAC = 90 + 45 = 135º

Certo Robson , ficou claro meu erro.

Voltei para acompanhar à sua resolução e não pairou nenhuma dúvida. grato um abraço



Raimundo

muito obrigado por solucionarem minha dúvida

Galera, fiz de uma maneira um pouco diferente. Observe: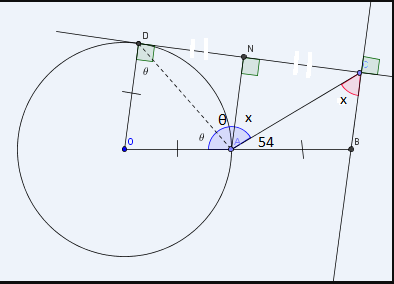 

DA=2rcosθ → NA=2rcos²θ → AC=(2rcos²θ )/(cos(x)). Resolvendo o sistema trigonometrico:


(r)/( sen(x) ) = ( 2.r.cos²θ )/(cos(x).sen(180-(54+x))


2θ +x=126