Computação Quantica/Mecanica quantica usando notação de Dirac
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Computação Quantica/Mecanica quantica usando notação de Dirac
por Enslavex Qui 26 Jan 2012, 14:38
Boas tardes, estou aqui resolvendo uns exercicios de preparação para a prova e deparei-me com um quebra-cabeças do tamanho do mundo! xD
Aqui vai:
"Considere os operadores de spin:
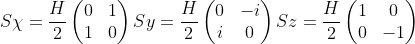
e vectores próprios de Sz:
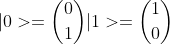
(a) Calcule a forma do operador S^2(ao quadrado)=(Sx)^2+(Sy)^2+(Sz)^2.
(b) Diga que efeito tem o operador S+=Sx+i*Sy sobre o estado |0>.
Como que eu faço esta coisa?!
Aqui vai:
"Considere os operadores de spin:
e vectores próprios de Sz:
(a) Calcule a forma do operador S^2(ao quadrado)=(Sx)^2+(Sy)^2+(Sz)^2.
(b) Diga que efeito tem o operador S+=Sx+i*Sy sobre o estado |0>.
Como que eu faço esta coisa?!
Enslavex- Iniciante
- Mensagens : 7
Data de inscrição : 24/01/2012
Idade : 37
Localização : Lisboa
Re: Computação Quantica/Mecanica quantica usando notação de Dirac
por Enslavex Sex 27 Jan 2012, 00:56
Ninguem percebe nada disto?!
Enslavex- Iniciante
- Mensagens : 7
Data de inscrição : 24/01/2012
Idade : 37
Localização : Lisboa
Re: Computação Quantica/Mecanica quantica usando notação de Dirac
por Dirac Sea Seg 26 Nov 2018, 20:07
Caro,
Certamente tarde demais para si, mas não tarde demais para outros.
O operador é calculado simplesmente fazendo:
S^2=S_x^2 + S_y^2 + S_z^2 = \frac{h^2}{4} \left[ \left(\begin{smallmatrix}
0 & 1 \\
1 &0
\end{smallmatrix}\right)^2 + \left(\begin{smallmatrix}
0 & -i \\
i &0
\end{smallmatrix}\right)^2 + \left(\begin{smallmatrix}
1 & 0 \\
0 & -1
\end{smallmatrix}\right)^2 \right] = \frac{3h^2}{4} \left(\begin{smallmatrix}
1 & 0 \\
0 & 1
\end{smallmatrix}\right)^2 = \\
= \frac{3h^2}{4} \mathbf{1}
O que não é mais do que multiplicação de matrizes.
A alínea b) é mais interessante. Primeiro construímos o operador S+:
S_+ = S_x + i S_y = \frac{h}{2} \left(\begin{smallmatrix}
0 & 1 \\
1 &0
\end{smallmatrix}\right) + i \frac{h}{2} \left(\begin{smallmatrix}
0 & -i \\
i &0
\end{smallmatrix}\right) = \\
= \frac{h}{2} \left(\begin{smallmatrix}
0 & 1 \\
1 &0
\end{smallmatrix}\right) + \frac{h}{2} \left(\begin{smallmatrix}
0 & 1 \\
-1 &0
\end{smallmatrix}\right) = h \left(\begin{smallmatrix}
0 & 1 \\
0 &0
\end{smallmatrix}\right)
Assim, temos que:
S_+ \left| 0 \right \rangle = h \left(\begin{smallmatrix}
0 & 1 \\
0 &0
\end{smallmatrix}\right) \left(\begin{smallmatrix}
0 \\
1
\end{smallmatrix}\right) = h \left(\begin{smallmatrix}
1 \\
0
\end{smallmatrix}\right) = h \left| 1 \right \rangle
Este operador S+ chama-se um raising operator porque "subiu" o estado de spin para um valor mais alto.
Certamente tarde demais para si, mas não tarde demais para outros.
O operador é calculado simplesmente fazendo:
0 & 1 \\
1 &0
\end{smallmatrix}\right)^2 + \left(\begin{smallmatrix}
0 & -i \\
i &0
\end{smallmatrix}\right)^2 + \left(\begin{smallmatrix}
1 & 0 \\
0 & -1
\end{smallmatrix}\right)^2 \right] = \frac{3h^2}{4} \left(\begin{smallmatrix}
1 & 0 \\
0 & 1
\end{smallmatrix}\right)^2 = \\
= \frac{3h^2}{4} \mathbf{1}
O que não é mais do que multiplicação de matrizes.
A alínea b) é mais interessante. Primeiro construímos o operador S+:
0 & 1 \\
1 &0
\end{smallmatrix}\right) + i \frac{h}{2} \left(\begin{smallmatrix}
0 & -i \\
i &0
\end{smallmatrix}\right) = \\
= \frac{h}{2} \left(\begin{smallmatrix}
0 & 1 \\
1 &0
\end{smallmatrix}\right) + \frac{h}{2} \left(\begin{smallmatrix}
0 & 1 \\
-1 &0
\end{smallmatrix}\right) = h \left(\begin{smallmatrix}
0 & 1 \\
0 &0
\end{smallmatrix}\right)
Assim, temos que:
0 & 1 \\
0 &0
\end{smallmatrix}\right) \left(\begin{smallmatrix}
0 \\
1
\end{smallmatrix}\right) = h \left(\begin{smallmatrix}
1 \\
0
\end{smallmatrix}\right) = h \left| 1 \right \rangle
Este operador S+ chama-se um raising operator porque "subiu" o estado de spin para um valor mais alto.
Dirac Sea- Iniciante
- Mensagens : 19
Data de inscrição : 24/11/2018
Idade : 31
Localização : Lisboa, Portugal
Conteúdo patrocinado
Tópicos semelhantes» Mecânica quântica
» Mecânica quântica
» Questão de Mecânica Quântica
» e Introdução à Mecânica Quântica
» Estrutura eletrônica/Mecânica Quântica
» Mecânica quântica
» Questão de Mecânica Quântica
» e Introdução à Mecânica Quântica
» Estrutura eletrônica/Mecânica Quântica
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
