Equaçoes redutíveis às fundamentais
4 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 2
Página 1 de 2 • 1, 2 
 Equaçoes redutíveis às fundamentais
Equaçoes redutíveis às fundamentais
sec²x=4/3 : Gabarito: S={x ∈ ℝ | x = ± pi/6 + k.2pi ou x= ± 5pi/6 + k.2pi ; k ∈ ℤ}
Nessa primeira eu só consegui chegar em : ±pi/6 + k.2pi
Como eu chego nesse x=±5pi/6+k.2pi ??
Sen²x=Cos²x : Gabarito: S={x ∈ ℝ | x= pi/4 + k.pi ou x= 3pi/4 + k.pi ; k ∈ ℤ}
Nessa segunda só consegui chegar no: x= pi/4 + k.pi
Como eu chego nesse x= 3pi/4 + k.pi ??
Nessa primeira eu só consegui chegar em : ±pi/6 + k.2pi
Como eu chego nesse x=±5pi/6+k.2pi ??
Sen²x=Cos²x : Gabarito: S={x ∈ ℝ | x= pi/4 + k.pi ou x= 3pi/4 + k.pi ; k ∈ ℤ}
Nessa segunda só consegui chegar no: x= pi/4 + k.pi
Como eu chego nesse x= 3pi/4 + k.pi ??

Douglas01- Recebeu o sabre de luz

- Mensagens : 155
Data de inscrição : 07/01/2022
Localização : São Paulo
Giovana Martins gosta desta mensagem
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
cos ² x = 3/4 então cosx = ±√3/2
senx = ±cosx então sen²x = 1 - sen²x ou sen²x = sen²x - 1
ok
senx = ±cosx então sen²x = 1 - sen²x ou sen²x = sen²x - 1
ok
Última edição por pedro de broglie em Sáb 13 Abr 2024, 17:33, editado 1 vez(es)

pedro de broglie- Padawan

- Mensagens : 93
Data de inscrição : 06/12/2021
Idade : 19
Localização : Campinas, SP
Giovana Martins gosta desta mensagem
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
tendi foi nada kkkpedro de broglie escreveu:cos ² x = 3/4 então cosx = ±√3/2
senx = ±cosx então senx = 1 - sen²x ou senx = sen²x - 1
ok

Douglas01- Recebeu o sabre de luz

- Mensagens : 155
Data de inscrição : 07/01/2022
Localização : São Paulo
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
[latex]\\\mathrm{sec^2(x)=\frac{4}{3}\to \frac{1}{cos^2(x)}=\frac{4}{3}\to cos^2(x)=\frac{3}{4}\therefore\ cos(x)=\pm \frac{\sqrt{3}}{2}}\\\\ \mathrm{Para\ cos(x)=-\frac{\sqrt{3}}{2}:cos(x)=cos\left ( \frac{5\pi }{6} \right )}\\\\ \mathrm{Da\ teoria\ cos(\alpha )=cos(\beta )\ \therefore\ \alpha =\pm \beta +2n\pi ,n\in \mathbb{Z}}\\\\ \mathrm{Assim:x=\pm \frac{5\pi }{6}+2n\pi ,n\in\mathbb{Z}}\\\\ \mathrm{Para\ cos(x)=\frac{\sqrt{3}}{2}:cos(x)=cos\left ( \frac{\pi }{6} \right )}\\\\ \mathrm{Da\ teoria\ cos(\alpha )=cos(\beta )\ \therefore\ \alpha =\pm \beta +2n\pi ,n\in \mathbb{Z}}\\\\ \mathrm{Assim:x=\pm \frac{\pi }{6}+2n\pi ,n\in\mathbb{Z}}\\\\ \mathrm{S=\left \{ x\in\mathbb{R}\ |\ \pm \frac{\pi }{6}+2n\pi \ ou\ \pm \frac{5\pi }{6}+2n\pi ,n\in\mathbb{Z} \right \}}[/latex]
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Douglas01 gosta desta mensagem
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
Veja as páginas 160, 165 e 169 do livro abaixo.
Fundamentos da Matemática Elementar: https://barbosadejesu.wordpress.com/wp-content/uploads/2021/09/fundamentos-da-matematica-elementar-3.pdf
As equações sin(x) = sin(y), cos(x) = cos(y) e tan(x) = tan(y) têm padrões.
Note que este padrões verificados nas páginas indicadas comportam exceções. Estas exceções estão na contabilização do 2kpi (mais comum) e do kpi (menos comum).
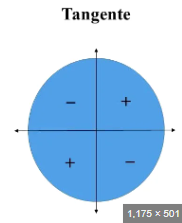
Ou seja, no geral você verá a resposta com o 2kpi embutido e às vezes aparecerá somente o kpi. Por que isto ocorre? Isto ocorre pois há ângulos que são côngruos a cada 180°, ao invés de 360°.
Por exemplo:
tan(x) = 1
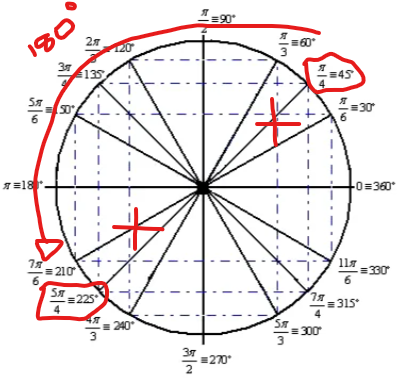
Se você disser que x = (pi/4) + 2kpi você está excluindo algumas soluções, pois o arco côngruo de pi/4 em se tratando de tangente é 5pi/4. De pi/4 até 5pi/4 você anda (5pi/4) - (pi/4) = pi = 180°, ou seja, você anda kpi, e não 2kpi no ciclo trigonométrico.
O correto, portanto, é x = (pi/4) + kpi.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Douglas01 gosta desta mensagem
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
A propósito, desculpe a qualidade das ilustrações. Hoje estou sem meu note para fazer os desenhos, daí não consigo fazer nada melhor que isso. Caso algo não tenha ficado claro, avise.
Fonte primeira imagem: Fonte.
Fonte segunda imagem: Fonte.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8544
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
Agora sim! haha. Agora deu pra ver onde eu errei. Na hora de estrair a raiz do cosseno eu só considerei o valor positivo e esqueci do negativo. Incrivel como um erro bobo te causa tanta dor de cabeça e perca de tempo kkk. ObrigadoGiovana Martins escreveu:[latex]\\\mathrm{sec^2(x)=\frac{4}{3}\to \frac{1}{cos^2(x)}=\frac{4}{3}\to cos^2(x)=\frac{3}{4}\therefore\ cos(x)=\pm \frac{\sqrt{3}}{2}}\\\\ \mathrm{Para\ cos(x)=-\frac{\sqrt{3}}{2}:cos(x)=cos\left ( \frac{5\pi }{6} \right )}\\\\ \mathrm{Da\ teoria\ cos(\alpha )=cos(\beta )\ \therefore\ \alpha =\pm \beta +2n\pi ,n\in \mathbb{Z}}\\\\ \mathrm{Assim:x=\pm \frac{5\pi }{6}+2n\pi ,n\in\mathbb{Z}}\\\\ \mathrm{Para\ cos(x)=\frac{\sqrt{3}}{2}:cos(x)=cos\left ( \frac{\pi }{6} \right )}\\\\ \mathrm{Da\ teoria\ cos(\alpha )=cos(\beta )\ \therefore\ \alpha =\pm \beta +2n\pi ,n\in \mathbb{Z}}\\\\ \mathrm{Assim:x=\pm \frac{\pi }{6}+2n\pi ,n\in\mathbb{Z}}\\\\ \mathrm{S=\left \{ x\in\mathbb{R}\ |\ \pm \frac{\pi }{6}+2n\pi \ ou\ \pm \frac{5\pi }{6}+2n\pi ,n\in\mathbb{Z} \right \}}[/latex]

Douglas01- Recebeu o sabre de luz

- Mensagens : 155
Data de inscrição : 07/01/2022
Localização : São Paulo
Giovana Martins gosta desta mensagem
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
Aliais, me desculpe, eu tinha entendido errado sua explicacao. x=3pi/4+k.pi nao existe entao?Giovana Martins escreveu:Veja as páginas 160, 165 e 169 do livro abaixo.Fundamentos da Matemática Elementar: https://barbosadejesu.wordpress.com/wp-content/uploads/2021/09/fundamentos-da-matematica-elementar-3.pdfAs equações sin(x) = sin(y), cos(x) = cos(y) e tan(x) = tan(y) têm padrões.Note que este padrões verificados nas páginas indicadas comportam exceções. Estas exceções estão na contabilização do 2kpi (mais comum) e do kpi (menos comum).Ou seja, no geral você verá a resposta com o 2kpi embutido e às vezes aparecerá somente o kpi. Por que isto ocorre? Isto ocorre pois há ângulos que são côngruos a cada 180°, ao invés de 360°.Por exemplo:tan(x) = 1Se você disser que x = (pi/4) + 2kpi você está excluindo algumas soluções, pois o arco côngruo de pi/4 em se tratando de tangente é 5pi/4. De pi/4 até 5pi/4 você anda (5pi/4) - (pi/4) = pi = 180°, ou seja, você anda kpi, e não 2kpi no ciclo trigonométrico.O correto, portanto, é x = (pi/4) + kpi.

Douglas01- Recebeu o sabre de luz

- Mensagens : 155
Data de inscrição : 07/01/2022
Localização : São Paulo
 Re: Equaçoes redutíveis às fundamentais
Re: Equaçoes redutíveis às fundamentais
Não
a) Para cosx = + √3/2 existem apenas duas soluções, na 1ª volta:
1) x = 30º = pi/6
2) x = 330º = 11.pi/6 = - pi/6
b) Para cosx = - √3/2 existem apenas duas soluções, na 1ª volta:
1) x = 150º = 5.pi/6
2) x = 210º = 7.pi/6
a) Para cosx = + √3/2 existem apenas duas soluções, na 1ª volta:
1) x = 30º = pi/6
2) x = 330º = 11.pi/6 = - pi/6
b) Para cosx = - √3/2 existem apenas duas soluções, na 1ª volta:
1) x = 150º = 5.pi/6
2) x = 210º = 7.pi/6

Elcioschin- Grande Mestre

- Mensagens : 73174
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Equações redutíveis às fundamentais
» Equações redutíveis às fundamentais 2° dúvida
» Dúvida sobre equações fundamentais
» Equações Redutíveis a 1º e 2º Grau
» Equações redutíveis ao segundo grau
» Equações redutíveis às fundamentais 2° dúvida
» Dúvida sobre equações fundamentais
» Equações Redutíveis a 1º e 2º Grau
» Equações redutíveis ao segundo grau
PiR2 :: Matemática :: Trigonometria
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos