Resolva um Triângulo
3 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 2
Página 1 de 2 • 1, 2 
 Resolva um Triângulo
Resolva um Triângulo
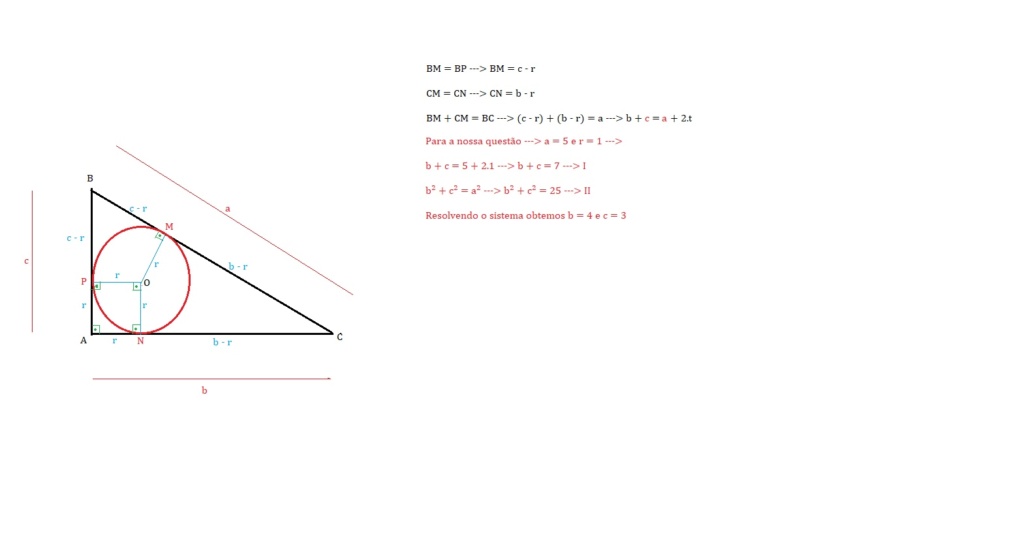
Resolva um triângulo retângulo ABC, sabendo que a=5 e r=1.
Obs: Acredito que r seja o raio da circunferência inscrita no triângulo
Obs: Acredito que r seja o raio da circunferência inscrita no triângulo
Luis_Moreira- Iniciante
- Mensagens : 3
Data de inscrição : 07/03/2024
Idade : 18
Giovana Martins gosta desta mensagem
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
r = (b + c - a)/2 ---> 1 = (b + c - 5)/2 ---> b + c = 7 ---> c = 7 - b ---> I
b² + c² = a² ---> b² + c² = 25 ---> II
I em II --> calcule b
Depois calcule c em I
b² + c² = a² ---> b² + c² = 25 ---> II
I em II --> calcule b
Depois calcule c em I

Elcioschin- Grande Mestre

- Mensagens : 73161
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Giovana Martins e Luis_Moreira gostam desta mensagem
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Posso estar equivocada, mas este enunciado está bem fajuto.
Se a hipotenusa for 5, logo, trata-se do triângulo pitagórico cuja terna é dada por (3,4,5) e assim está resolvido o triângulo.
Partindo-se do princípio de que trata-se de uma circunferência inscrita ao triângulo e que 5 é um dos catetos, pelo Teorema de Poncelet:
a + b = c + 2r, tal que c é a hipotenusa do triângulo retângulo. Assim:
5 + b = c + 2, o que acarreta c - b = 3 (i).
Pelo Teorema de Pitágoras:
a2 + b2 = c2, tal que c2 - b2 = 25 (ii)
De (i) e (ii): b = 8/3 e c = 17/3.
Assim, (a,b,c) = (5, 8/3, 17/3).
Última edição por Giovana Martins em Qui 07 Mar 2024, 22:59, editado 1 vez(es)
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Postei, pois eu já havia digitado.
Fiz de um jeito supondo que a = 5 não é hipotenusa, pois o triângulo retângulo de hipotenusa 5 tem catetos 3 e 4 (isso a gente sabe sem fazer contas pelo fato de o triângulo ser famoso, mas deveria ser provado tal como o Élcio fez).
Optei por explorar a questão de outra forma. Enfim, o enunciado me é estranho.
A meu ver, ambas as formas estão corretas. Deixo para ti a tarefa de provar isso (sem muito rigor) a partir da relação S = pr, sendo S a área do triângulo, p o semiperímetro e r o raio da circunferência inscrita.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo

Elcioschin- Grande Mestre

- Mensagens : 73161
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Giovana Martins gosta desta mensagem
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Boa tarde, mestre. Espero que o senhor esteja bem.
Na verdade, eu desenvolvi a questão de um modo um pouquinho diferente em relação à forma como o senhor desenvolveu. O senhor partiu do princípio de que a = 5 é hipotenusa. A forma que eu propus parte da ideia de que a = 5 é um dos catetos.
Não vejo problemas em fazer desta forma, pois o enunciado deixa margem para interpretação de que a = 5 é um dos catetos, uma vez que ele não diz que a = 5 é hipotenusa.
Eu enunciei o Teorema de Poncelet como sendo a + b = c + 2r. Neste caso, c seria a hipotenusa. Veja que ao fim da minha resolução eu obtive a terna (a,b,c) = (5, 8/3, 17/3), sendo c = 17/3 o maior lado justamente por ser a hipotenusa do triângulo.
Substituindo a terna (a,b,c) em a + b = c + 2r encontra-se r = 1 tal como o enunciado indicou.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Agora entendi seu ponto de vista.
Eu considerei a = 5 a hipotenusa, por vício, já que na maioria das vezes, é o que as questões consideram, pelo menos no Brasil.
Mas nada impede que a = 5 seja um dos catetos.
Isto deveria ter sido esclarecido no enunciado. Note que o colega que postou estava em dúvida até sobre r ser ou não o raio do círculo inscrito!
Só quem pode esclarecer é quem postou a questão.
Eu considerei a = 5 a hipotenusa, por vício, já que na maioria das vezes, é o que as questões consideram, pelo menos no Brasil.
Mas nada impede que a = 5 seja um dos catetos.
Isto deveria ter sido esclarecido no enunciado. Note que o colega que postou estava em dúvida até sobre r ser ou não o raio do círculo inscrito!
Só quem pode esclarecer é quem postou a questão.

Elcioschin- Grande Mestre

- Mensagens : 73161
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Elcioschin escreveu:Agora entendi seu ponto de vista.
Eu considerei a = 5 a hipotenusa, por vício, já que na maioria das vezes, é o que as questões consideram, pelo menos no Brasil.
Mas nada impede que a = 5 seja um dos catetos.
Isto deveria ter sido esclarecido no enunciado. Note que o colega que postou estava em dúvida até sobre r ser ou não o raio do círculo inscrito!
Só quem pode esclarecer é quem postou a questão.
Pois é, mestre. A primeira resolução que eu pensei foi no triângulo pitagórico também e acredito até que seja isso que a questão queria, mas o enunciado, a meu ver, não está muito bom. Ele deixa muitas brechas.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Infelizmente o enunciado da questão é exatamente o que escrevi. O livro antes de chegar nessas questões demonstra alguns teoremas, e nesses teoremas utiliza 'r' como o raio da circunferência inscrita e 'a' como a hipotenusa do triangulo.Elcioschin escreveu:Agora entendi seu ponto de vista.
Eu considerei a = 5 a hipotenusa, por vício, já que na maioria das vezes, é o que as questões consideram, pelo menos no Brasil.
Mas nada impede que a = 5 seja um dos catetos.
Isto deveria ter sido esclarecido no enunciado. Note que o colega que postou estava em dúvida até sobre r ser ou não o raio do círculo inscrito!
Só quem pode esclarecer é quem postou a questão.
Essa questão foi retirado do livro Fundamentos de Matemática Elementar Vol. 3, existe uma versão desse livro feito para professores onde existe a resolução escrita dos exercícios. Tentei entender ler essa resolução, mas ela possuiu um salto logico que não consegui compreender.
Segue a parte da resolução que não compreendi:
(a+b+c)/2*r = a*h/2 => h = (2r^2+2ra)/a => h=12/5
Acho interessante dizer que a formula que o mestre usou (r=[b+c-a]/2) não foi mostrado no livro, talvez por ser um livro de trigonometria que possui apenas um apêndice reservado para a resolução de triângulos.
Luis_Moreira- Iniciante
- Mensagens : 3
Data de inscrição : 07/03/2024
Idade : 18
 Re: Resolva um Triângulo
Re: Resolva um Triângulo
Luis_Moreira escreveu:Elcioschin escreveu:Agora entendi seu ponto de vista.Eu considerei a = 5 a hipotenusa, por vício, já que na maioria das vezes, é o que as questões consideram, pelo menos no Brasil.Mas nada impede que a = 5 seja um dos catetos.Isto deveria ter sido esclarecido no enunciado. Note que o colega que postou estava em dúvida até sobre r ser ou não o raio do círculo inscrito!Só quem pode esclarecer é quem postou a questão.Infelizmente o enunciado da questão é exatamente o que escrevi. O livro antes de chegar nessas questões demonstra alguns teoremas, e nesses teoremas utiliza 'r' como o raio da circunferência inscrita e 'a' como a hipotenusa do triangulo.Essa questão foi retirado do livro Fundamentos de Matemática Elementar Vol. 3, existe uma versão desse livro feito para professores onde existe a resolução escrita dos exercícios. Tentei entender ler essa resolução, mas ela possuiu um salto logico que não consegui compreender.Segue a parte da resolução que não compreendi:(a+b+c)/2*r = a*h/2 => h = (2r^2+2ra)/a => h=12/5Acho interessante dizer que a formula que o mestre usou (r=[b+c-a]/2) não foi mostrado no livro, talvez por ser um livro de trigonometria que possui apenas um apêndice reservado para a resolução de triângulos.
Ah, entendido. Na verdade é uma questão do contexto do livro. Eu também usei o FME e, de fato, nele há algumas questões assim, que fazem sentido dentro do contexto do livro.
O teorema que o Élcio usou é o Teorema de Poncelet. Tem esse teorema no FME de geometria plana, porém, não com esse nome. Caso tenha interesse, procure pelo Youtube esse nome que você achará algumas demonstrações. Elas são bem tranquilas de entender.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Resolva o Triângulo
» Resolva a equacao x^2 – 9x + 8 = 0, agora resolva....
» resolva
» Resolva em ℝ
» resolva
» Resolva a equacao x^2 – 9x + 8 = 0, agora resolva....
» resolva
» Resolva em ℝ
» resolva
PiR2 :: Matemática :: Trigonometria
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos