Equações de retas perpendiculares dados três pontos
3 participantes
Página 1 de 1
 Equações de retas perpendiculares dados três pontos
Equações de retas perpendiculares dados três pontos
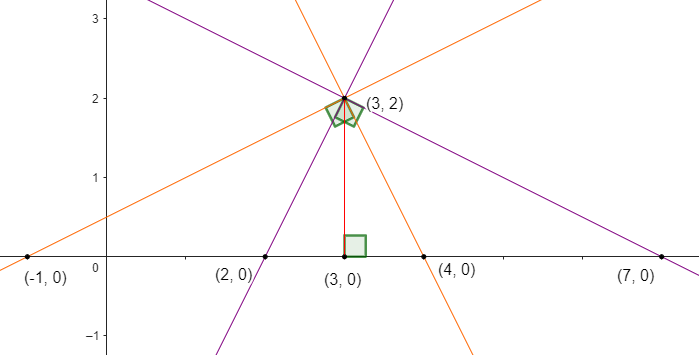
II.27) As retas r e s são perpendiculares e passam pelo ponto A (3;2) . Sendo B e C os pontos onde r e s cortam o eixo das abscissas, determine as equações de r e s sabendo que a medida do segmento BC é 5.
R:
y = 2x -4 e y = -x/2 + 7/2
ou
y = -2x + 8 e y = x/2 + 1/2
R:
y = 2x -4 e y = -x/2 + 7/2
ou
y = -2x + 8 e y = x/2 + 1/2
Última edição por vvarmbruster em Dom Nov 26 2023, 00:43, editado 1 vez(es)
vvarmbruster- Recebeu o sabre de luz

- Mensagens : 100
Data de inscrição : 10/11/2022
Giovana Martins gosta desta mensagem
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
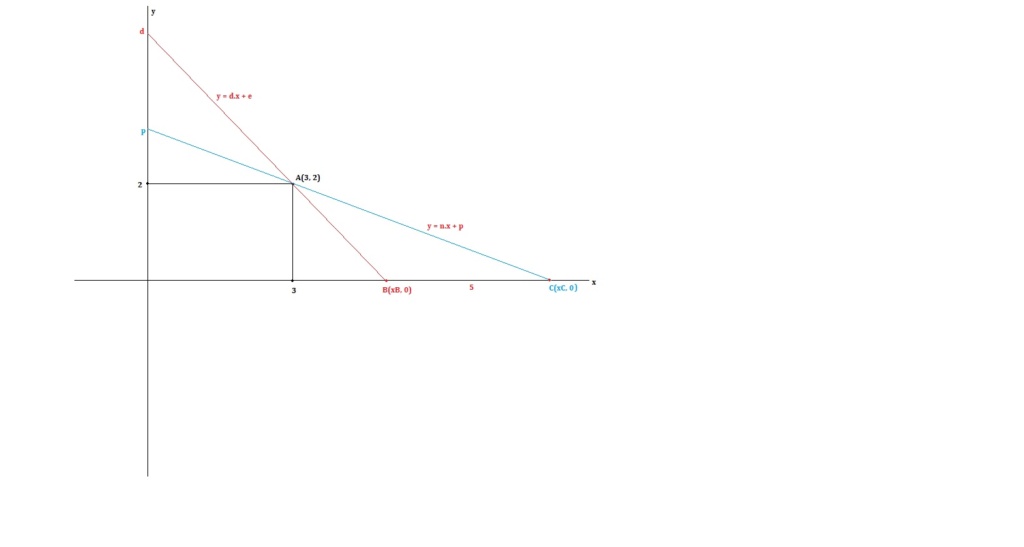
Reta r ---> y = d.x + e ---> Passa por (3, 2) e (xB, 0) ---> d = coeficiente angular
2 = 3.d + e ---> I
0 = xB.d + e --> II
I - II ---> 2 = (3 - xB).d ---> d = 2/(3 - xB) ---> III
Reta s ---> y = n.x + p ---> Passa por (3, 2) e (xC, 0) ---> n = - 1/d coeficiente angular
2 = 3.n + p ---> 2 = 3.(-1/d) + p ---> IV
0 = xC.n + p --> 0 = xC/(-1/d) + p --> V
IV - V ---> 2 = (3 - xC).(-1/d) ---> d = (xC - 3)/2 ---> VI
VI = III ---> (xC - 3)/2 = 2/(3 - xB) ----> VII ---> relação entre xB e xC
xC - xB = 5 ---> VIII ---> Outra relação entre xB e xC
Calcule xB e xC e complete
2 = 3.d + e ---> I
0 = xB.d + e --> II
I - II ---> 2 = (3 - xB).d ---> d = 2/(3 - xB) ---> III
Reta s ---> y = n.x + p ---> Passa por (3, 2) e (xC, 0) ---> n = - 1/d coeficiente angular
2 = 3.n + p ---> 2 = 3.(-1/d) + p ---> IV
0 = xC.n + p --> 0 = xC/(-1/d) + p --> V
IV - V ---> 2 = (3 - xC).(-1/d) ---> d = (xC - 3)/2 ---> VI
VI = III ---> (xC - 3)/2 = 2/(3 - xB) ----> VII ---> relação entre xB e xC
xC - xB = 5 ---> VIII ---> Outra relação entre xB e xC
Calcule xB e xC e complete


Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Giovana Martins e vvarmbruster gostam desta mensagem
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
Sejam os pontos A(3,2), B(m,0) e C(n,0), tal que m < n. Sem muito rigor, tendo em vista que de início não conhecemos as abscissas m e n, plote os pontos A, B e C no sistema xOy.
Após fazer o esboço das localizações dos pontos A, B e C, note que será formado o triângulo ABC de base BC = 5 e altura cujo comprimento corresponde à ordenada do ponto A, isto é, 2. Sendo BC = 5 e h = 2, logo, a área do triângulo ABC é 5.
Do triângulo ABC, tem-se:
[latex]\\\mathrm{[ABC]=\frac{1}{2}\begin{Vmatrix} 3 &2 &1 \\ \mathrm{m} & 0 &1 \\ \mathrm{n} &0 &1 \end{Vmatrix}=5\ \therefore\ |-2m+2n|=10\ (i)}[/latex]
Seja P(3,0) tal que AP = h. Note que m(∠APC) = m(∠CAP) = 90°. Dada esta configuração, pelas relações métricas no triângulo retângulo, tem-se: (AP)² = BP x PC.
Manipulando a última igualdade obtida:
(3 - m)(n - 3) = 4 (ii)
De (i) e (ii), tem-se:
(m,n) = {(-1,4), (2,7), (4,-1), (7,2)}
Dos pares ordenados (m,n) obtidos, note que (4,-1) e (7,2) tem de ser descartados, tendo em vista que de início estabelecemos a condição m < n. Logo, os possíveis pares (m,n) são (m,n) = {(-1,4), (2,7)}.
Para (m,n) = (-1,4) tem-se B(-1,0) e C(4,0);
Para (m,n) = (2,7) tem-se B(2,0) e C(7,0).
Agora que sabemos quais são os pares ordenados (m,n) que satisfazem o enunciado, basta determinarmos todas as possíveis retas. Veja:
[latex]\\\mathrm{Para\ A(3,2)\ e\ B(-1,0)\to y=\frac{x}{2}+\frac{1}{2}}\\\\ \mathrm{Para\ A(3,2)\ e\ C(4,0)\to y=-2x+8}\\\\ \mathrm{\ Para\ A(3,2)\ e\ B(2,0)\to y=2x-4}\\\\ \mathrm{Para\ A(3,2)\ e\ C(7,0)\to y=-\frac{x}{2}+\frac{7}{2}}[/latex]
Se houver dúvidas, avise.
Última edição por Giovana Martins em Sáb Nov 25 2023, 20:13, editado 1 vez(es)
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
Medeiros gosta desta mensagem
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
Postei, pois eu já havia digitado.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
Elcioschin escreveu:Reta r ---> y = d.x + e ---> Passa por (3, 2) e (xB, 0) ---> d = coeficiente angular
2 = 3.d + e ---> I
0 = xB.d + e --> II
I - II ---> 2 = (3 - xB).d ---> d = 2/(3 - xB) ---> III
Reta s ---> y = n.x + p ---> Passa por (3, 2) e (xC, 0) ---> n = - 1/d coeficiente angular
2 = 3.n + p ---> 2 = 3.(-1/d) + p ---> IV
0 = xC.n + p --> 0 = xC/(-1/d) + p --> V
IV - V ---> 2 = (3 - xC).(-1/d) ---> d = (xC - 3)/2 ---> VI
VI = III ---> (xC - 3)/2 = 2/(3 - xB) ----> VII ---> relação entre xB e xC
xC - xB = 5 ---> VIII ---> Outra relação entre xB e xC
Calcule xB e xC e complete
Muito obrigado, mestre!
vvarmbruster- Recebeu o sabre de luz

- Mensagens : 100
Data de inscrição : 10/11/2022
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
Giovana Martins escreveu:Sejam os pontos A(3,2), B(m,0) e C(n,0), tal que m < n. Sem muito rigor, tendo em vista que de início não conhecemos as abscissas m e n, plote os pontos A, B e C no sistema xOy.Após fazer o esboço das localizações dos pontos A, B e C, note que será formado o triângulo ABC de base BC = 5 e altura cujo comprimento corresponde à ordenada do ponto A, isto é, 2. Sendo BC = 5 e h = 2, logo, a área do triângulo ABC é 5.Do triângulo ABC, tem-se:[latex]\\\mathrm{[ABC]=\frac{1}{2}\begin{Vmatrix} 3 &2 &1 \\ \mathrm{m} & 0 &1 \\ \mathrm{n} &0 &1 \end{Vmatrix}=5\ \therefore\ |-2m+2n|=10\ (i)}[/latex]Seja P(3,0) tal que AP = h. Note que m(∠APC) = m(∠CAP) = 90°. Dada esta configuração, pelas relações métricas no triângulo retângulo, tem-se: (AP)² = BP x PC.Manipulando a última igualdade obtida:(3 - m)(n - 3) = 4 (ii)De (i) e (ii), tem-se:(m,n) = {(-1,4), (2,7), (4,-1), (7,2)}Dos pares ordenados (m,n) obtidos, note que (4,-1) e (7,2) tem de ser descartados, tendo em vista que de início estabelecemos a condição m < n. Logo, os possíveis pares (m,n) são (m,n) = {(-1,4), (2,7)}.Para (m,n) = (-1,4) tem-se B(-1,0) e C(4,0);Para (m,n) = (2,7) tem-se B(2,0) e C(7,0).Agora que sabemos quais são os pares ordenados (m,n) que satisfazem o enunciado, basta determinarmos todas as possíveis retas. Veja:[latex]\\\mathrm{Para\ A(3,2)\ e\ B(-1,0)\to y=\frac{x}{2}+\frac{1}{2}}\\\\ \mathrm{Para\ A(3,2)\ e\ C(4,0)\to y=-2x+8}\\\\ \mathrm{\ Para\ A(3,2)\ e\ B(2,0)\to y=2x-4}\\\\ \mathrm{Para\ A(3,2)\ e\ C(7,0)\to y=-\frac{x}{2}+\frac{7}{2}}[/latex]Se houver dúvidas, avise.
Explodiu minha mente, hahaaha. Muito obrigado pela ajuda!
Uma dúvida: a condição m < n é um pressuposto para auxiliar na resolução do exercício ou é alguma coisa que o exercício garante em alguma parte que eu acabei perdendo?
vvarmbruster- Recebeu o sabre de luz

- Mensagens : 100
Data de inscrição : 10/11/2022
Giovana Martins gosta desta mensagem
 Re: Equações de retas perpendiculares dados três pontos
Re: Equações de retas perpendiculares dados três pontos
Disponha.
O m < n é porque eu fixei o ponto B antes do ponto C, ou seja, o ponto B está mais próximo da origem do que o ponto C, logo, a abscissa m do ponto B obrigatoriamente será menor que a abscissa n do ponto C.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
vvarmbruster gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Distância Entre Pontos em Retas Perpendiculares
» Retas Perpendiculares
» Dados três pontos não-colineares A,B,C
» [RIHAN - 2012] Um Ponto. Dois Pontos: Três Pontos...
» Retas perpendiculares
» Retas Perpendiculares
» Dados três pontos não-colineares A,B,C
» [RIHAN - 2012] Um Ponto. Dois Pontos: Três Pontos...
» Retas perpendiculares
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos