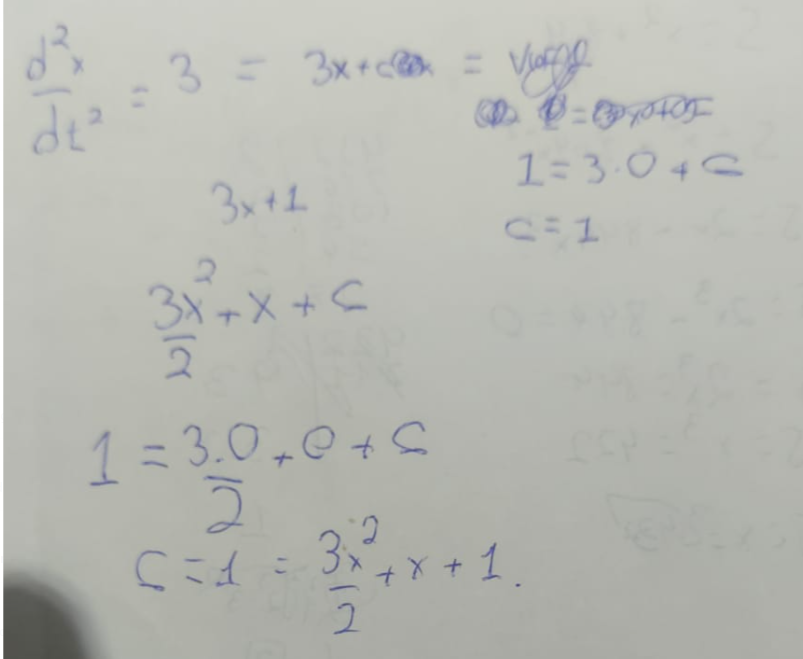Calculo da Posição usando integral
3 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Calculo da Posição usando integral
Calculo da Posição usando integral
Uma partícula se desloca sobre o eixo x com
uma função posição x = x(t). Determine x = x(t)
sabendo que:
[latex]\frac {d^2x}{dt^2} = 3\\ v(0) = 1 \\x(0) = 1 [/latex]
Minha dúvida é como começar, eu vi vários vídeos mas não ensina a integrar derivada nesse tipo.
Nesse caso como é uma derivada '' tenho que integrar 2x?
Pelo que eu entendi, se foi derivada 2x esse valor deveria representar a aceleração não ?
as primeiras eu entendi a lógica e consegui fazer:
mas dps xD
[latex] \frac {dx}{dt} = 2t-1\\x(0) = 2 \\ \int 2t-1 = t^2-t+c \\ f(0)=2 = \\ 0^2 + 0 + c = 2 \\ c=2 \\ = t^2-t+2 [/latex]
uma função posição x = x(t). Determine x = x(t)
sabendo que:
[latex]\frac {d^2x}{dt^2} = 3\\ v(0) = 1 \\x(0) = 1 [/latex]
Minha dúvida é como começar, eu vi vários vídeos mas não ensina a integrar derivada nesse tipo.
Nesse caso como é uma derivada '' tenho que integrar 2x?
Pelo que eu entendi, se foi derivada 2x esse valor deveria representar a aceleração não ?
as primeiras eu entendi a lógica e consegui fazer:
mas dps xD
[latex] \frac {dx}{dt} = 2t-1\\x(0) = 2 \\ \int 2t-1 = t^2-t+c \\ f(0)=2 = \\ 0^2 + 0 + c = 2 \\ c=2 \\ = t^2-t+2 [/latex]
ReplayBr- Jedi

- Mensagens : 284
Data de inscrição : 30/01/2013
Idade : 31
Localização : São Bernardo do Campo
 Re: Calculo da Posição usando integral
Re: Calculo da Posição usando integral
Para a derivada segunda ser uma constante, x(t) é uma função do 2º grau
x(t) = a.t² + b.t + c
x(0) = 1 ---> 1 = a.0² + b.0 + c ---> c = 1
x'(t) = 2.a.t + b ---> v(t) = 2.at + b ---> v(0) = 1 ---> 1 = 2.a.0 + b ---> b = 1
x"(t) = 2.a ---> 3 = 2.a ---> a = 3/2
x(t) = (3/2).t² + t + 1
x(t) = a.t² + b.t + c
x(0) = 1 ---> 1 = a.0² + b.0 + c ---> c = 1
x'(t) = 2.a.t + b ---> v(t) = 2.at + b ---> v(0) = 1 ---> 1 = 2.a.0 + b ---> b = 1
x"(t) = 2.a ---> 3 = 2.a ---> a = 3/2
x(t) = (3/2).t² + t + 1

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Calculo da Posição usando integral
Re: Calculo da Posição usando integral
Mestre acho que sou ansioso kkk, consegui fazer aqui.Elcioschin escreveu:Para a derivada segunda ser uma constante, x(t) é uma função do 2º grau
x(t) = a.t² + b.t + c
x(0) = 1 ---> 1 = a.0² + b.0 + c ---> c = 1
x'(t) = 2.a.t + b ---> v(t) = 2.at + b ---> v(0) = 1 ---> 1 = 2.a.0 + b ---> b = 1
x"(t) = 2.a ---> 3 = 2.a ---> a = 3/2
x(t) = (3/2).t² + t + 1
Mas não sei se foi do jeito certo, eu fiz integrando 1 vez, e adicionando +1 de constante que veio do (v) = 1, e dps eu integrei e adicionei a que veio do (x) = 1
Pelo que eu entendi, quando eu integrei eu estou pegando a velocidade e depois a posição, certo ?
ReplayBr- Jedi

- Mensagens : 284
Data de inscrição : 30/01/2013
Idade : 31
Localização : São Bernardo do Campo
ReplayBr- Jedi

- Mensagens : 284
Data de inscrição : 30/01/2013
Idade : 31
Localização : São Bernardo do Campo
 Re: Calculo da Posição usando integral
Re: Calculo da Posição usando integral
O que você fez está correto. O que você tem é uma equação diferencial. As igualdades v(0) = 1 e x(0) = 1 são chamadas de condições de contorno, que são justamente utilizadas para encontrar as constantes provenientes das integrações que fazemos ao longo da resolução.
Do jeito que o Élcio fez é um pouquinho mais rápido.
[latex]\\\mathrm{Derivada\ de\ 2^a\ ordem\ constante,logo,x(t)=at^2+bt+c}\\\\ \mathrm{\frac{dx(t)}{dt}=v(t)=2at+b\ \therefore\ \frac{d^2x(t)}{dt^2}=\frac{d}{dt}\left ( \frac{dx(t)}{dt} \right )=\frac{d}{dt}(2at+b)=2a}\\\\ \mathrm{Sendo\ \frac{d^2x(t)}{dt^2}=3,logo,2a=3\ \therefore\ a=\frac{3}{2}}\\\\ \mathrm{Voltando\ em\ v(t)=2at+b\ \therefore\ v(t)=3t+b.\ Do\ enunciado:v(0)=1}\\\\ \mathrm{\therefore\ 1=3\times 0+b, o\ que\ acarreta\ b=1\ tal\ que\ v(t)=3t+1}\\\\ \mathrm{Dado\ que\ (a,b)=\left ( \frac{3}{2},1 \right ),tem-se\ x(t)=\frac{3}{2}t^2+t+c.\ Do\ enunciado\ x(0)=1}\\\\ \mathrm{\therefore\ 1=\frac{3}{2}\times 0^2+0+c,o\ que\ acarreta\ c=1\ tal\ que\ x(t)=\frac{3}{2}t^2+t+1}[/latex]
Última edição por Giovana Martins em Qua 15 Nov 2023, 12:01, editado 1 vez(es)
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Calculo da Posição usando integral
Re: Calculo da Posição usando integral
Editei o post.
Postei porque eu já havia digitado.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8527
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» usando integral dupla calcule a área da região limitada (Calculo integral)
» Usando integral dupla calcule a área da região (Calculo integral)
» Cálculo de área usando integral
» C.M usando integral
» Usando integral dupla
» Usando integral dupla calcule a área da região (Calculo integral)
» Cálculo de área usando integral
» C.M usando integral
» Usando integral dupla
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos