questão de geometria plana
2 participantes
Página 1 de 1
questão de geometria plana
por rebecaszz Seg 06 Mar 2023, 19:35
Seja x um número real positivo tal que [latex]x=1+\frac{1}{x}[/latex]. Considere o quadrado EFGH a seguir, formado por quatro retângulos de lados x e [latex]\frac{1}{x}[/latex]e um quadrilátero central ABCD.
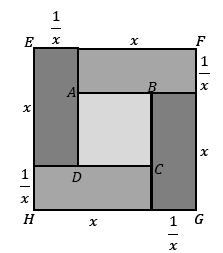
a) Mostre que ABCD é um quadrado unitário, ou seja, mostre que os quatro ângulos internos são retos e que os lados têm medida unitária. Determine, então, a área de EFGH.
b) O quadrado EFGH tem lado de medida ax −b, em que a e b são números inteiros positivos. Calcule esses valores.
c) Encontre o valor de x.
a) Mostre que ABCD é um quadrado unitário, ou seja, mostre que os quatro ângulos internos são retos e que os lados têm medida unitária. Determine, então, a área de EFGH.
b) O quadrado EFGH tem lado de medida ax −b, em que a e b são números inteiros positivos. Calcule esses valores.
c) Encontre o valor de x.
Última edição por rebecaszz em Ter 07 Mar 2023, 08:59, editado 1 vez(es)
rebecaszz- Recebeu o sabre de luz
- Mensagens : 101
Data de inscrição : 21/02/2023
Idade : 19
Localização : campinas, sp
Re: questão de geometria plana
por DaoSeek Ter 07 Mar 2023, 06:47
(a) os lados de ABCD são paralelos aos de EFGH, daí os angulos são retos. Pra calcular a medida de cada lado basta subtrair do lado de EFGH as medidas das "bordas":
\(AB = \dfrac 1x + x - \dfrac 1x - \dfrac 1x = x - \dfrac 1x = 1\)
(b) Como \( \dfrac 1x = x-1 \) segue que \( \dfrac 1x +x = 2x -1\). Portanto a = 2 e b = 1.
(c) \(x = \dfrac 1x + 1 \implies x^2 -x-1 = 0 \implies x = \dfrac{1 \pm \sqrt 5}2 \implies x = \dfrac{1 + \sqrt 5}2\)
\(AB = \dfrac 1x + x - \dfrac 1x - \dfrac 1x = x - \dfrac 1x = 1\)
(b) Como \( \dfrac 1x = x-1 \) segue que \( \dfrac 1x +x = 2x -1\). Portanto a = 2 e b = 1.
(c) \(x = \dfrac 1x + 1 \implies x^2 -x-1 = 0 \implies x = \dfrac{1 \pm \sqrt 5}2 \implies x = \dfrac{1 + \sqrt 5}2\)
DaoSeek- Jedi
- Mensagens : 316
Data de inscrição : 29/07/2022
rebecaszz gosta desta mensagem
Tópicos semelhantes» Questão de Geometria Plana
» Questão de Geometria Plana
» Questão geometria plana
» Questão de Geometria Plana
» Questão - Geometria Plana
» Questão de Geometria Plana
» Questão geometria plana
» Questão de Geometria Plana
» Questão - Geometria Plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
