Questão de Geometria Plana

por Glauber Damasceno Ter 30 Out 2012, 22:28

Considere um Quadrado CDEF e um triângulos equilátero ABC , de lados iguais a 1 + 2√3, liga-se o vértice E , do quadrado, ao vértice A , do triângulo , originando a diagonal do retângulo por eles formados . O ponto em que a diagonal intercepta o lado DC é H e o ponto em que ela intercepta o lado BC é G. Calcule o comprimento do segmento CG .

Desde já agradeço aos amigos .

por **Elcioschin** Qui 01 Nov 2012, 15:59

Glauber

Confesso que não conseguí entender o enunciado:
Visualizei o quadrado e o triângulo.
Entendí também a união dos vértices A do triângulo e E do quadrado.
E os dois vértices C, são os mesmos?
Qual é o retângulo formado?

Poderia expicar melhor?
Existe uma figura desta questão? Se xistir, poste-a por favor.

por **Medeiros** Qui 01 Nov 2012, 19:26

É um quadrado e um triângulo lado a lado, com as bases alinhadas sobre a mesma reta suporte. Esta questão já esteve por aqui mas não achei na busca.

por **raimundo pereira** Qui 01 Nov 2012, 19:58

https://pir2.forumeiros.com/t33966-abcd-e-um-quadrado-e-o-cef-e-equilatero?highlight=abcd+e+um+quadrado

Medeiros acho que você está falando desse problema?

por **Elcioschin** Qui 01 Nov 2012, 20:22

Glauber

Como você pode ver, seu enunciado não está correto: não existe nenhum retângulo e nenhuma diagonal.

Por favor, quando postar um enunciado, poste-o exatamente como o orignal, e não como você acha que é.

por **Medeiros** Sex 02 Nov 2012, 01:26

Raimundo, é esse problema mesmo. Só que, pelo que me lembre, é de postagem bem mais antiga e teve um iluminado paciente que o resolveu por geom. euclidiana. Ainda não tinha visto a sua resolução, neste.

por **raimundo pereira** Sex 02 Nov 2012, 11:09

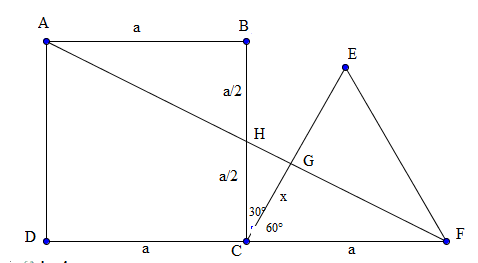
da semelhança dos triângulos FHC e AFD temos BH=HC=a/2
S∆ GFC + S∆GHC = S∆HFC

(a*x*sen60°)/2 + (a/2*x*sen30°)/2= (a/2 * a)/2

(a*x*V3/2)/2 + (a/2*x *1/2)/2= a²/4

a*xV3/4 + a*x/4=a²/4

a*xV3 +a*x=a²
a*x(V3+1)=a²
x=a/V3+1
x=a(V3-1)/2