Permutação de caminhos possíveis- Passe Ufms
2 participantes
Página 1 de 1
 Permutação de caminhos possíveis- Passe Ufms
Permutação de caminhos possíveis- Passe Ufms
Passe Ufms 3 etapa -Um estudante está em sua casa e pretende ir de bicicleta até a UFMS. A figura a seguir mostra os possíveis caminhos que ele pode percorrer, sendo que poderá pedalar ao longo dos quadrados pretos, mas não pode pedalar por eles e pode seguir pedalando apenas para baixo ou à direita. De quantas maneiras diferentes pode ele ir de casa à UFMS?
A) 40. B) 56. C) 66. D) 70. E) 126.
Gabarito oficial: 66
A) 40. B) 56. C) 66. D) 70. E) 126.
Gabarito oficial: 66
pradebon05- Iniciante
- Mensagens : 15
Data de inscrição : 29/10/2022
 Re: PERMUTAÇÃO DE CAMINHOS POSSÍVEIS- PASSE UFMS
Re: PERMUTAÇÃO DE CAMINHOS POSSÍVEIS- PASSE UFMS
Fala, Prade.
Fica difícil contabilizar a quantidade de caminhos pelos quais ele não passa pelo quadrado preto diretamente, então vamos tentar outra estratégia:
Vamos contar a quantidade de caminhos totais, como se não tivesse o quadrado preto, e tirar os casos em que ele passa pelo quadrado preto. Para os casos totais, ele teria que andar para a direita 5 vezes e para baixo 4 vezes. Podemos pensar nisso como uma permutação com repetição:
Imagine que você está fazendo um manual de instrução para o ciclista ler, onde D significa que ele tem que ir para a direita e B para baixo, uma das maneiras que você poderia construir esse manual seria:
DDDDDBBBB
ou também: DBDBDBDDB
Assim, basta fazer uma permutação de repetição com todos os B's e D's:
[latex]P = \frac{9!}{5!.4!} = 126[/latex]
Agora, vamos encontrar os caminhos pelos quais o ciclista passa pelo quadrado preto:
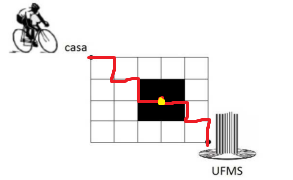
Basta que ele passe pelo ponto amarelo acima. O problema é a mesma permutação com repetição, primeiro devemos fazer um manual com 3 D (direitas) e 2 B (baixos), seguido de um manual de 2 D e 2 B.:
Isso dá:
[latex]P_1 . P_2 = \frac{5!}{2!.3!}.\frac{4!}{2!2!} = 60[/latex]
Tirando 60 de 126, temos 66.
Fica difícil contabilizar a quantidade de caminhos pelos quais ele não passa pelo quadrado preto diretamente, então vamos tentar outra estratégia:
Vamos contar a quantidade de caminhos totais, como se não tivesse o quadrado preto, e tirar os casos em que ele passa pelo quadrado preto. Para os casos totais, ele teria que andar para a direita 5 vezes e para baixo 4 vezes. Podemos pensar nisso como uma permutação com repetição:
Imagine que você está fazendo um manual de instrução para o ciclista ler, onde D significa que ele tem que ir para a direita e B para baixo, uma das maneiras que você poderia construir esse manual seria:
DDDDDBBBB
ou também: DBDBDBDDB
Assim, basta fazer uma permutação de repetição com todos os B's e D's:
[latex]P = \frac{9!}{5!.4!} = 126[/latex]
Agora, vamos encontrar os caminhos pelos quais o ciclista passa pelo quadrado preto:

Basta que ele passe pelo ponto amarelo acima. O problema é a mesma permutação com repetição, primeiro devemos fazer um manual com 3 D (direitas) e 2 B (baixos), seguido de um manual de 2 D e 2 B.:
Isso dá:
[latex]P_1 . P_2 = \frac{5!}{2!.3!}.\frac{4!}{2!2!} = 60[/latex]
Tirando 60 de 126, temos 66.
João Pedro Lima- Jedi

- Mensagens : 220
Data de inscrição : 02/01/2022
Idade : 22
Localização : Rio de Janeiro, RJ
 Re: Permutação de caminhos possíveis- Passe Ufms
Re: Permutação de caminhos possíveis- Passe Ufms
João Pedro Lima escreveu:Fala, Prade.
Fica difícil contabilizar a quantidade de caminhos pelos quais ele não passa pelo quadrado preto diretamente, então vamos tentar outra estratégia:
Vamos contar a quantidade de caminhos totais, como se não tivesse o quadrado preto, e tirar os casos em que ele passa pelo quadrado preto. Para os casos totais, ele teria que andar para a direita 5 vezes e para baixo 4 vezes. Podemos pensar nisso como uma permutação com repetição:
Imagine que você está fazendo um manual de instrução para o ciclista ler, onde D significa que ele tem que ir para a direita e B para baixo, uma das maneiras que você poderia construir esse manual seria:
DDDDDBBBB
ou também: DBDBDBDDB
Assim, basta fazer uma permutação de repetição com todos os B's e D's:
[latex]P = \frac{9!}{5!.4!} = 126[/latex]
Agora, vamos encontrar os caminhos pelos quais o ciclista passa pelo quadrado preto:
Basta que ele passe pelo ponto amarelo acima. O problema é a mesma permutação com repetição, primeiro devemos fazer um manual com 3 D (direitas) e 2 B (baixos), seguido de um manual de 2 D e 2 B.:
Isso dá:
[latex]P_1 . P_2 = \frac{5!}{2!.3!}.\frac{4!}{2!2!} = 60[/latex]
Tirando 60 de 126, temos 66.
Agradeço demais !!!
pradebon05- Iniciante
- Mensagens : 15
Data de inscrição : 29/10/2022
João Pedro Lima gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Caminhos possíveis
» Permutação Vs permutação circular(ajuda com )
» Probabilidade - Caminhos
» Quantos caminhos diferentes são possíveis?
» Passe 2021- Altura de um agrupamento de esferas
» Permutação Vs permutação circular(ajuda com )
» Probabilidade - Caminhos
» Quantos caminhos diferentes são possíveis?
» Passe 2021- Altura de um agrupamento de esferas
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












