Relação entre àreas - geometria plana

por Elnath Qua 19 Out 2022, 06:58

Nesta figura, o ponto E pertence à diagonal do retângulo ABCD, e a área do triângulo ACE tem 12 cm². Qual é a área do triângulo CDE, em cm²?

=Gabarito: 12 cm²

^{=Obrigada desde já}

Relação entre àreas - geometria plana Questz10

por catwopir Qua 19 Out 2022, 07:46

Aoba!

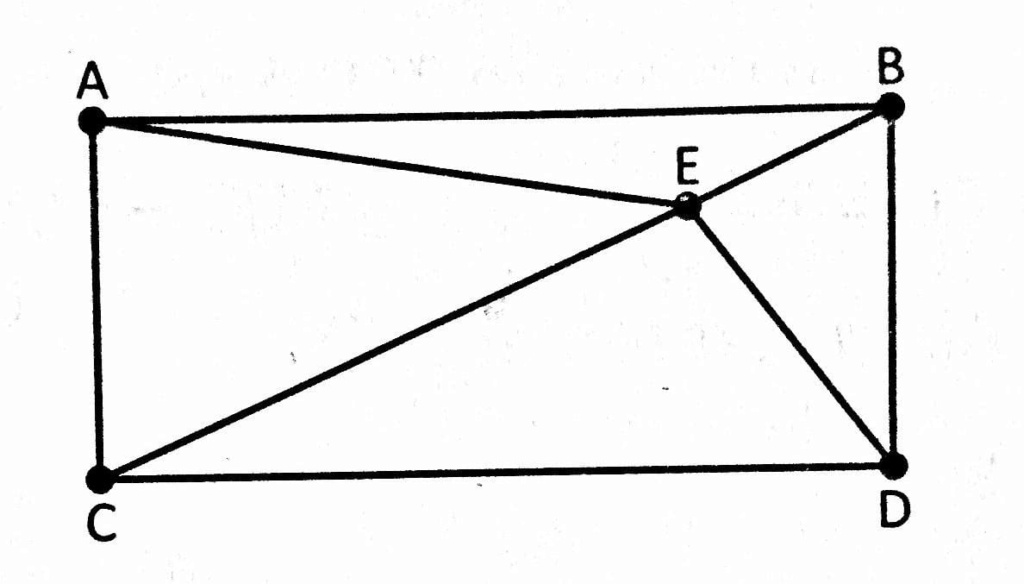
traçando a altura de todos os triângulos, temos:

O lado AB=A e AC=B

S_ACE=B.H/2
S_CED=A.H'/2
S_EBD=B.(A-H)/2
S_AEB=A(B-H')/2

S_ABC=AB/2

S_CBD=AB/2

S_ABC=S_ACE+S_AEB

S_CBD=S_CED+S_EBD

S_ACE+S_AEB=S_CED+S_EBD

S_ACE+(AB/2-AH'/2)=S_CED+(BA/2-BH/2)

S_ACE=S_CED+(AH'/2-BH/2)

Temos que AH'/2=S_CED e BH/2=S_ACE

S_ACE=S_CED+S_CED-S_ACE

S_ACE=S_CED

Creio ser isso, questãozinha puxada essa.

por Elnath Qua 19 Out 2022, 09:55

Muito obrigada! Razz

por **Medeiros** Qua 19 Out 2022, 19:00

É interessante notar -- e pode-se provar -- que enquanto o ponto E excursiona através da diagonal BC, sempre teremos a seguinte relação entre áreas:
-- [ACE] = [CDE]
-- [ABE] = [BDE]

por Elnath Qui 20 Out 2022, 07:09

Medeiros escreveu:É interessante notar -- e pode-se provar -- que enquanto o ponto E excursiona através da diagonal BC, sempre teremos a seguinte relação entre áreas:
-- [ACE] = [CDE]
-- [ABE] = [BDE]

Não sabia dessa relação! Obrigada por explicar!! Smile