Equações paramétricas da reta

3. Determine as equações paramétricas da reta s em cada caso:
(a) s passa pelo ponto (1, 2) e é perpendicular à reta 2x − 5y = 2.
(b) s é paralela à reta 2x + 5y = 1 e passa pelo ponto (1, 2).

Gabarito:
(a) s : x = 1 + 2t
             y = 2 − 5t,  t ∈ R.
(b) s :  x = 1 − 5t
              y = 2 + 2t,  t ∈ R.

Boa noite! Estudando equações paramétricas, me encontrei um pouco confusa em relação a essa questão. Alguém poderia me ajudar? Obrigada desde já.

Fala, Hypatia.
É possível analisar definindo os vetores diretores da reta e trabalhando com as condições dadas. Vai dar conta, mas é o jeito de fazer no espaço Rn.

O que vou demonstrar aqui vale para o R2 e diminui bastante as contas:
1) Se a reta r1: y = ax + b e a reta r2: y = cx + d são perpendiculares, então a*c = -1.

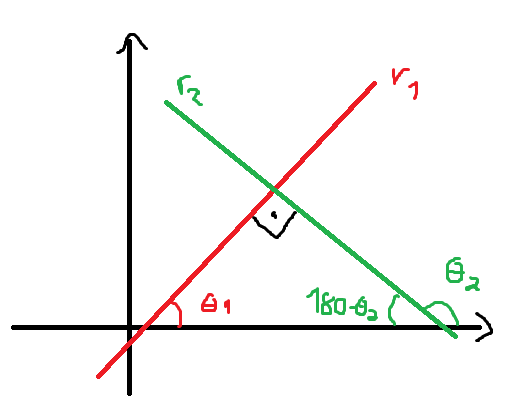
Repare que Theta1 e 180-Theta2 são complementares, assim:
[latex]\theta_1 + 180 - \theta_2 = 90[/latex]
[latex]\theta_1 + 90 = \theta_2[/latex]

Aplicando tangente dos dois lados:
[latex]tg(\theta_1 + 90) = tg(\theta_2)[/latex]
[latex]\frac{-1}{tg(\theta_1)} = tg(\theta_2)[/latex]

Como essas tangentes são definidas como os coeficientes angulares da reta, temos:
[latex]c.a = -1[/latex]

2) Se duas retas são paralelas, então possuem o mesmo coeficiente angular:


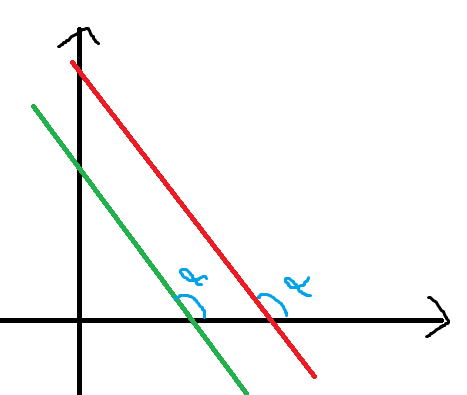
Pelas condições de paralelismo acima, sai direto que as retas possuem coeficientes angulares iguais.

Dito isso, eu faria a questão assim:

a) A reta 2x - 5y = 2 em sua forma reduzida é y = 2x/5 -2/5. Pela condição de perpendicularidade, sendo s = ax + b, temos:
2a/5 = -1 -> a = -5/2

Como a reta passa por (1,2):
2 = -5*1/2 + b -> b =9/2

Temos que s tem equação y = -5x/2 + 9/2 que na forma geral ficaria 2y + 5x - 9 = 0. Para encontrar a reta paramétrica é só fatorar de uma forma que você suma com os coeficientes de x e y:
5x - 9 = -2y
Soma 4 dos dois lados:
5x - 5 = -2y + 4
5(x-1) = -2(y-2)
(x-1)/2 = (y-2)/-5 = t

-> (x-1)/2 = t -> (x-1) = 2t -> x = 2t + 1
-> (y-2) = -5t -> y = -5t + 2

Fiz desse jeito só para convergir com o gabarito, mas há várias formas equivalentes de representar as equações paramétricas, você pode ter ficado com dúvida nisso. Você não precisa achar o mesmo valor que o gabarito. Olha:
5x - 9 = -2y
Subtrai 6 dos dois lados
5x - 15 = -2y - 6
5(x-3) = -2(y+3) 
(x-3)/-2 = (y+3)/5 = t

-> x-3 = -2t -> x = 3 -2t
-> y+3 = 5t -> y = 5t - 3

b) Pela condição de paralelismo, a reta s tem coeficiente angular = -2/5
Como passa por (1,2):
2 = -2*1/5 + b
b = 12/5

s: y = -2x/5 + 12/5
5y = -2x + 12
5y - 10 = -2x + 2
5(y-2) = -2(x-1)
(y-2)/2 = (x-1)/-5 = t

-> y - 2 = 2t ->  y = 2t + 2
-> x - 1 = -5t -> x = 1 - 5t

Ótima resolução. Obrigada.