FME - Parábola
2 participantes
Página 1 de 1
FME - Parábola
por Jvictors021 Dom 20 Mar 2022, 20:27
é dada a parábola de equação y = x2 em coordenadas cartesianas ortogonais. Sendo A = (a, a2); B = (b,b2) e X = (x, x2) tr~es pontos distintos da parábola:
A) Determine a área do triângulo ABX
B) Para cada x, distindo de a e de b, seja f(x) a área (positiva) do triângulo ABX, esboce o gráfico da função f
C) Determine o valor de x para o qual f(x) é máximo local (ou relativo)
GAB:
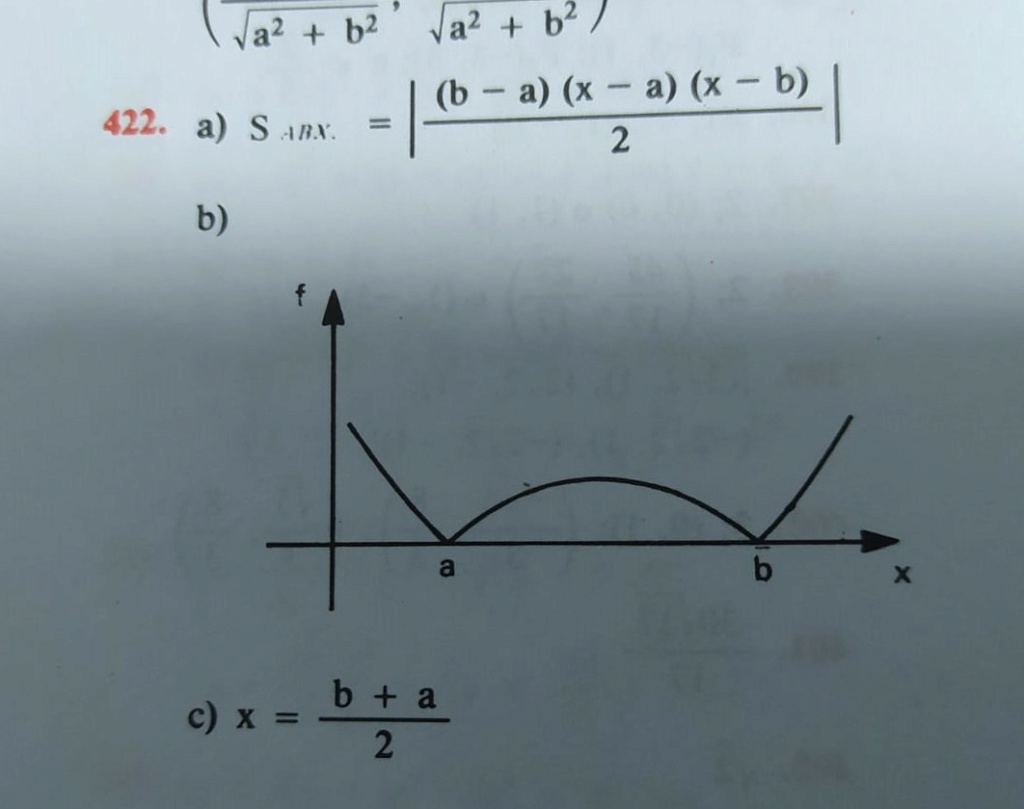
A) Determine a área do triângulo ABX
B) Para cada x, distindo de a e de b, seja f(x) a área (positiva) do triângulo ABX, esboce o gráfico da função f
C) Determine o valor de x para o qual f(x) é máximo local (ou relativo)
GAB:
Jvictors021- Estrela Dourada
- Mensagens : 1116
Data de inscrição : 02/07/2021
Idade : 21
Localização : Passa Quatro - MG
Re: FME - Parábola
por qedpetrich Seg 21 Mar 2022, 00:47
Olá Jvictor;
A) Utilizando o dispositivo prático matricial, temos:
Desenvolvendo a expressão obtida:
Dessa forma, S é igual a:
B) Pode analisar a partir do resultado obtido no item anterior, ou analisar essa função que significa a mesmíssima coisa, em seguida esboce um gráfico:
C) Aplique as Relações de Girard, vou recorrer ao cálculo diferencial:
A) Utilizando o dispositivo prático matricial, temos:
Desenvolvendo a expressão obtida:
Dessa forma, S é igual a:
B) Pode analisar a partir do resultado obtido no item anterior, ou analisar essa função que significa a mesmíssima coisa, em seguida esboce um gráfico:
C) Aplique as Relações de Girard, vou recorrer ao cálculo diferencial:
____________________________________________
Dê tempo ao
Lateralus Φ
qedpetrich- Monitor
- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
Jvictors021 gosta desta mensagem
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
