Paralelogramo no R3

por macaquinho da kipling Dom 06 Mar 2022, 15:54

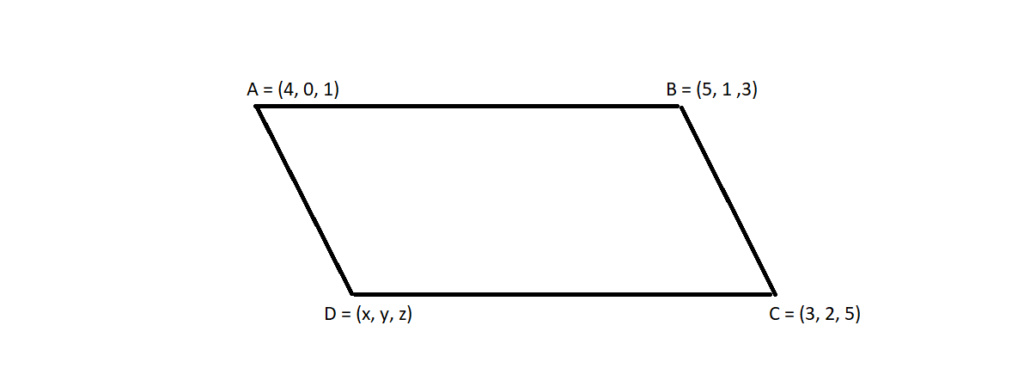
Se os pontos A(4,0,1), B(5,1,3), C(3,2,5) e D(x,y,z) são vértices de um paralelogramo ABCD, então a soma das coordenadas do vértice D é igual a?

Resp.: Sem gabarito.

Eu montei o plano cartesiano no R3, e com as coordenadas dos pontos dados, a gente pode pensar que:
1. AC = BD
2. AB = CD

Eu usei da primeira equação mesmo.
--------------------------
AC = BD
C - A = D - B
D = B + C - A = (5,1,3) + (3,2,5) - (4,0,1) = (8,3, Cool

- (4,0,1) = (4,3,7)

Somando as coordenadas: 4 +3 + 7 = 14

Fiz certo?
Obrigada!

por **Rory Gilmore** Dom 06 Mar 2022, 16:21

Está errado. Eu fiz uma resolução, caso não entenda alguma coisa me avise.

[latex]\overrightarrow{AD}[/latex] = (x - 4, y, z - 1)
[latex]\overrightarrow{BC}[/latex] = (- 2, 1, 2)

Impomos a igualdade entre as componentes dos dois vetores acima:
x - 4 = - 2
y = 1
z - 1 = 2

Logo:
x = 2
y = 1
z = 3

E o ponto D = (2, 1, 3)