retas simétricas em relação ao eixo das ordenadas

por JohnnyC Dom 20 Fev 2022, 01:16

Determine a equação da reta t, simétrica da reta (r) x + 2y - 4 = 0, em relação ao eixo das ordenadas.

R: x - 2y + 4 = 0

Novamente, pessoal, meu livro não explicou como resolve esse tipo de modelo de questão. Poderiam ajudar ? obrigado

por **Giovana Martins** Dom 20 Fev 2022, 01:53

A ideia desta é a mesma dessa daqui: https://pir2.forumeiros.com/t190819-retas-simetricas-entre-si#659864

Aqui vale destacar que quando o enunciado diz "em relação ao eixo das ordenadas" isto quer dizer que a simetria se dá em torno de y=0. Logo:

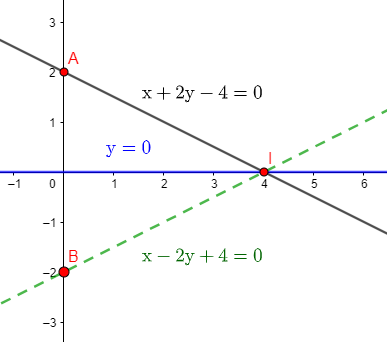
retas simétricas em relação ao eixo das ordenadas Oie_t118

Note que as curvas r e y=0 interceptam em I. Pela simetria, a curva t deve passar pelos pontos B e I.

por JohnnyC Dom 20 Fev 2022, 16:02

Muito obrigado pela ajuda, Gi!!! cheers

por **Giovana Martins** Dom 20 Fev 2022, 16:06

Disponha, Johnny Smile

. A propósito, eu terei de ajustar esta resolução, pois eu troquei os enunciados sem querer em relação àquela resolução que o Medeiros sugeriu um ajuste. Assim que eu puder eu ajusto!

por JohnnyC Dom 20 Fev 2022, 21:46

Gi, eu corrigi aqui e me confirma se eu estou certo, por favor.

A intersecção das retas irá ocorrer em y = 2, sendo que a reta r corta o eixo x em x = 4, enquanto que a reta t corta o eixo x em x = -4.

(r): reta decrescente
(t): reta crescente

Fazendo isso, a gente chega na equação da reta t. Fiz assim, estou certo ?

por **Giovana Martins** Sex 04 Mar 2022, 19:04

JohnnyC escreveu:Gi, eu corrigi aqui e me confirma se eu estou certo, por favor.

A intersecção das retas irá ocorrer em y = 2, sendo que a reta r corta o eixo x em x = 4, enquanto que a reta t corta o eixo x em x = -4.

(r): reta decrescente
(t): reta crescente

Fazendo isso, a gente chega na equação da reta t. Fiz assim, estou certo ?

Oiii, Johnny! Me perdoe a demora. Estava bem corrido por aqui. É exatamente isso que eu queria ter feito.